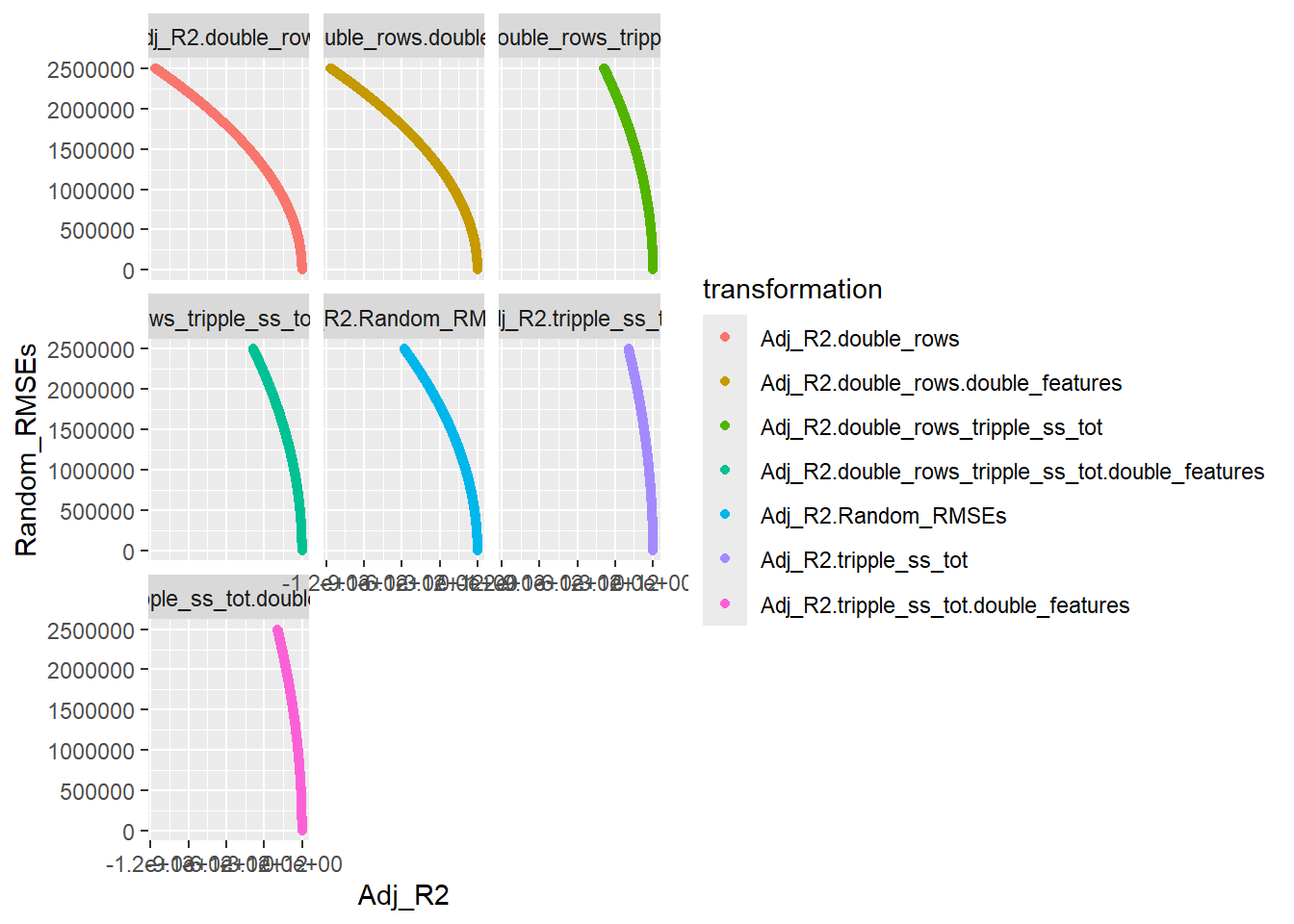
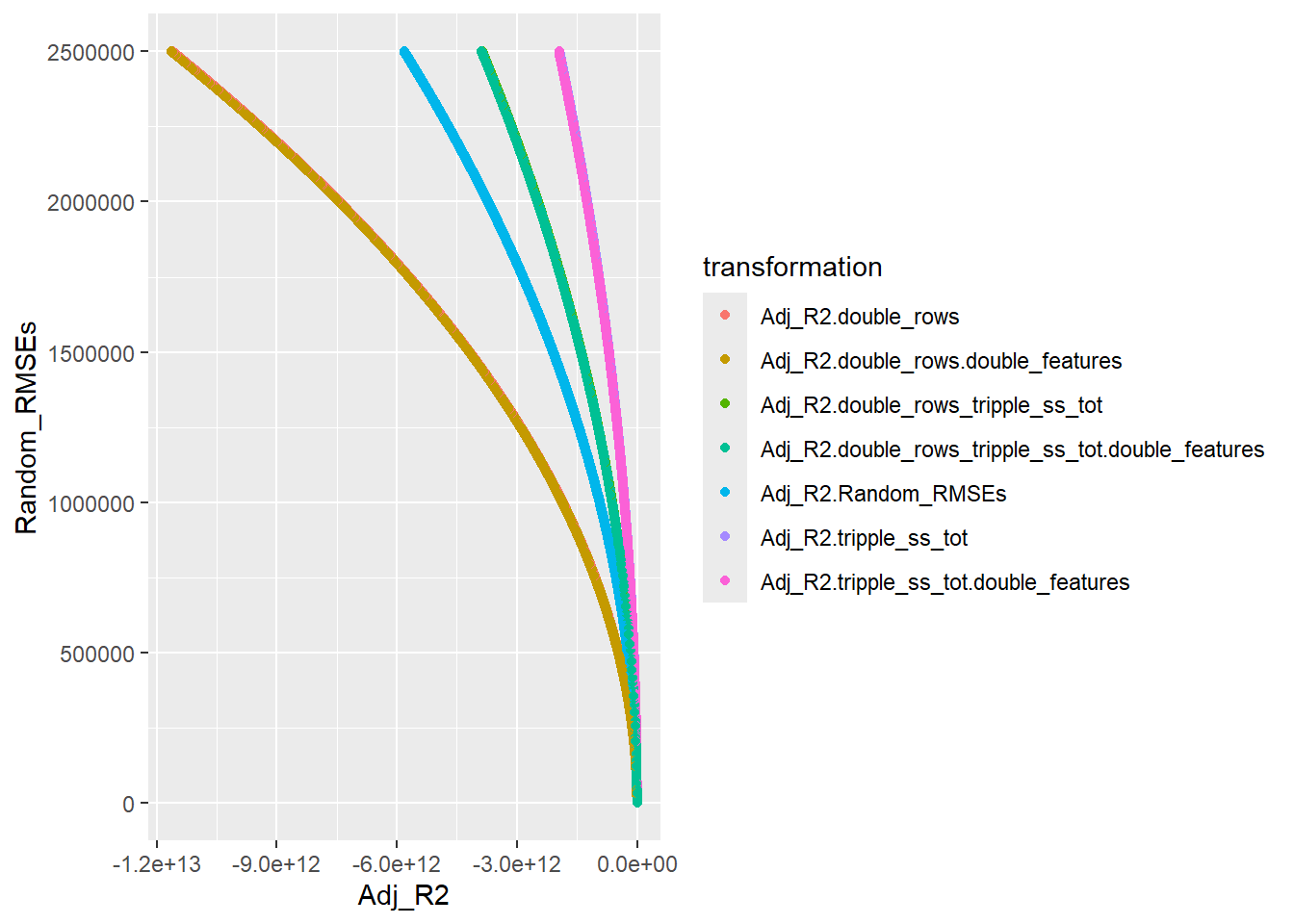
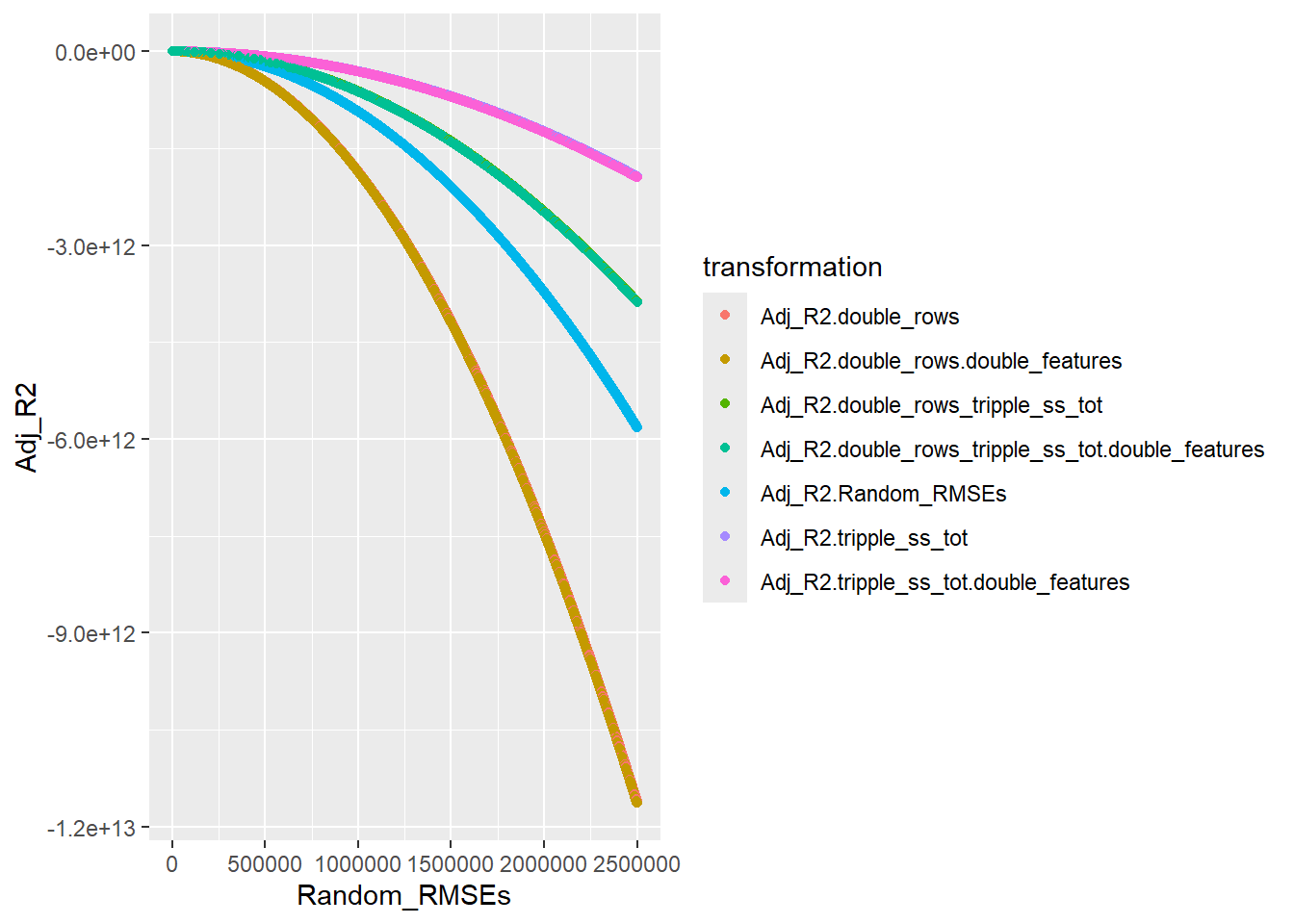
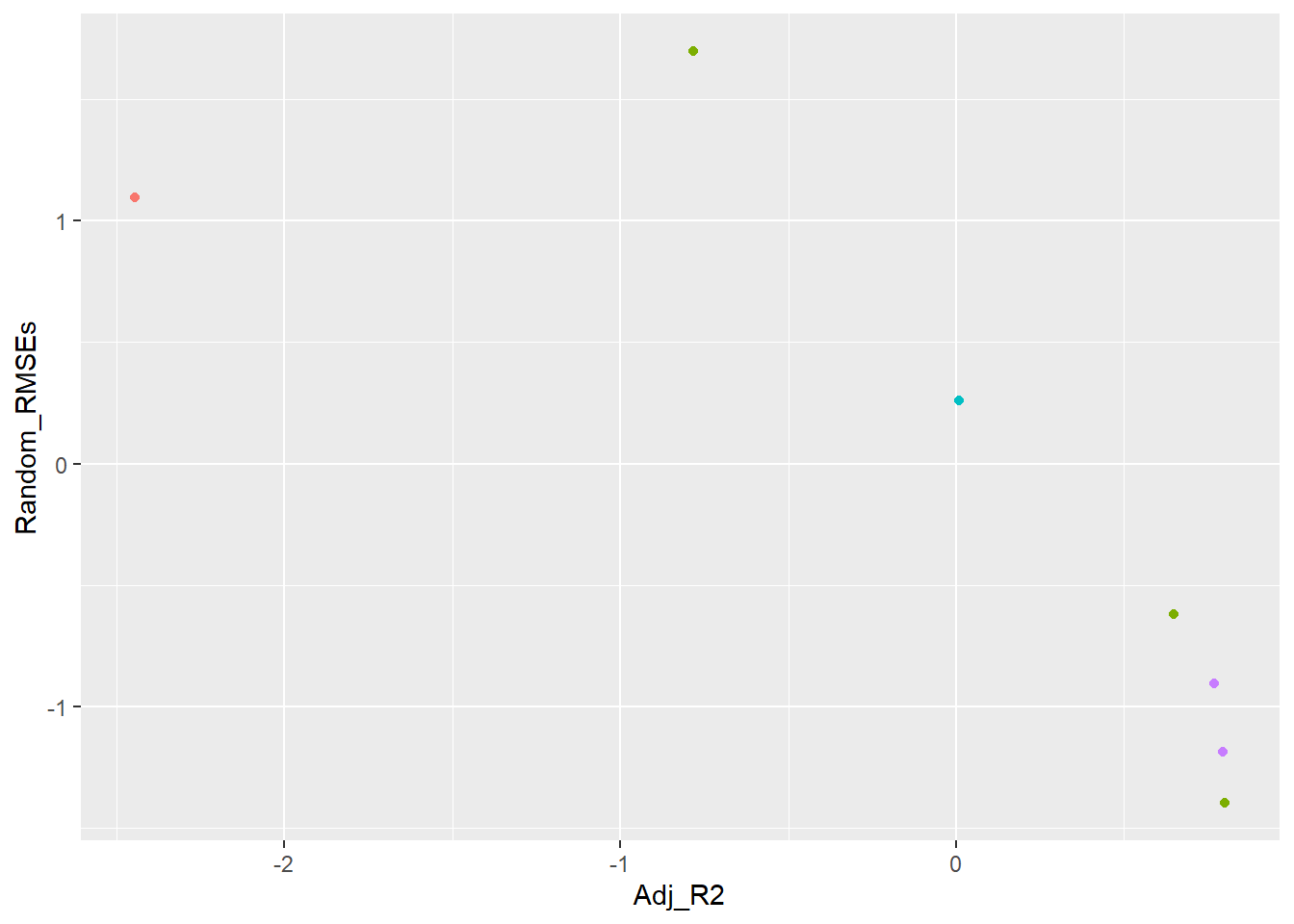
19  Adjusted R2 VS Root Mean Squared Error

19.1 Setup

── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
✔ dplyr     1.1.4     ✔ readr     2.1.5
✔ forcats   1.0.0     ✔ stringr   1.5.1
✔ ggplot2   3.5.1     ✔ tibble    3.2.1
✔ lubridate 1.9.3     ✔ tidyr     1.3.1
✔ purrr     1.0.2     
── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag()    masks stats::lag()
ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors
Loading required package: lattice

Attaching package: 'caret'

The following object is masked from 'package:purrr':

    lift
diab_pop <- readRDS('C:/Users/jkyle/Documents/GitHub/Intro_Jeff_Data_Science/DATA/diab_pop.RDS') %>%
  select(-seqn)

glimpse(diab_pop)
Rows: 5,719
Columns: 9
$ riagendr <fct> Male, Male, Male, Female, Female, Female, Male, Female, Male,…
$ ridageyr <dbl> 62, 53, 78, 56, 42, 72, 22, 32, 56, 46, 45, 30, 67, 67, 57, 8…
$ ridreth1 <fct> Non-Hispanic White, Non-Hispanic White, Non-Hispanic White, N…
$ dmdeduc2 <fct> College grad or above, High school graduate/GED, High school …
$ dmdmartl <fct> Married, Divorced, Married, Living with partner, Divorced, Se…
$ indhhin2 <fct> "$65,000-$74,999", "$15,000-$19,999", "$20,000-$24,999", "$65…
$ bmxbmi   <dbl> 27.8, 30.8, 28.8, 42.4, 20.3, 28.6, 28.0, 28.2, 33.6, 27.6, 2…
$ diq010   <fct> Diabetes, No Diabetes, Diabetes, No Diabetes, No Diabetes, No…
$ lbxglu   <dbl> NA, 101, 84, NA, 84, 107, 95, NA, NA, NA, 84, NA, 130, 284, 3…

19.1.1 Let’s try to predict lbxglu:

target <- 'lbxglu'

df <- diab_pop %>% 
  na.omit()

my_factor_vars <- df %>% select_if(is.factor) %>% colnames()

df_as_nums <- df %>%
  mutate_at(vars(my_factor_vars), as.integer) %>%
  mutate_at(vars(my_factor_vars), as.factor)
Warning: Using an external vector in selections was deprecated in tidyselect 1.1.0.
ℹ Please use `all_of()` or `any_of()` instead.
  # Was:
  data %>% select(my_factor_vars)

  # Now:
  data %>% select(all_of(my_factor_vars))

See <https://tidyselect.r-lib.org/reference/faq-external-vector.html>.
glimpse(df_as_nums)
Rows: 1,876
Columns: 9
$ riagendr <fct> 1, 1, 2, 1, 2, 1, 2, 2, 2, 1, 1, 2, 2, 1, 2, 1, 2, 2, 2, 1, 1…
$ ridageyr <dbl> 53, 78, 72, 45, 67, 67, 57, 24, 68, 66, 56, 37, 20, 24, 80, 7…
$ ridreth1 <fct> 3, 3, 1, 5, 2, 4, 2, 5, 1, 3, 3, 2, 4, 3, 2, 3, 4, 1, 1, 4, 2…
$ dmdeduc2 <fct> 3, 3, 2, 2, 5, 5, 1, 5, 1, 5, 1, 4, 3, 4, 1, 5, 4, 1, 3, 3, 4…
$ dmdmartl <fct> 3, 1, 4, 5, 1, 2, 4, 5, 3, 6, 1, 1, 5, 3, 2, 6, 5, 5, 1, 5, 1…
$ indhhin2 <fct> 4, 5, 13, 10, 6, 5, 5, 1, 4, 10, 4, 13, 13, 6, 3, 10, 6, 3, 4…
$ bmxbmi   <dbl> 30.8, 28.8, 28.6, 24.1, 43.7, 28.8, 35.4, 25.3, 33.5, 34.0, 2…
$ diq010   <fct> 2, 1, 2, 2, 2, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1…
$ lbxglu   <dbl> 101, 84, 107, 84, 130, 284, 398, 95, 111, 113, 397, 100, 94, …

19.1.2 preProcess 

pP <- preProcess(df_as_nums, c('center','scale')) 

df_as_nums <- predict(pP,df_as_nums) 

glimpse(df_as_nums)
Rows: 1,876
Columns: 9
$ riagendr <fct> 1, 1, 2, 1, 2, 1, 2, 2, 2, 1, 1, 2, 2, 1, 2, 1, 2, 2, 2, 1, 1…
$ ridageyr <dbl> 0.15617810, 1.59749118, 1.25157604, -0.30504208, 0.96331342, …
$ ridreth1 <fct> 3, 3, 1, 5, 2, 4, 2, 5, 1, 3, 3, 2, 4, 3, 2, 3, 4, 1, 1, 4, 2…
$ dmdeduc2 <fct> 3, 3, 2, 2, 5, 5, 1, 5, 1, 5, 1, 4, 3, 4, 1, 5, 4, 1, 3, 3, 4…
$ dmdmartl <fct> 3, 1, 4, 5, 1, 2, 4, 5, 3, 6, 1, 1, 5, 3, 2, 6, 5, 5, 1, 5, 1…
$ indhhin2 <fct> 4, 5, 13, 10, 6, 5, 5, 1, 4, 10, 4, 13, 13, 6, 3, 10, 6, 3, 4…
$ bmxbmi   <dbl> 0.20545760, -0.08208648, -0.11084088, -0.75781505, 2.06011687…
$ diq010   <fct> 2, 1, 2, 2, 2, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1…
$ lbxglu   <dbl> -0.30006288, -0.70905532, -0.15571260, -0.70905532, 0.3976301…
dV.df <- dummyVars( ~ . , 
                   data = df_as_nums, 
                   fullRank=TRUE)

df_dV <- as_tibble(predict(dV.df,df_as_nums)) 



features <- colnames(df_dV)[!colnames(df_dV) %in% c('seqn' , target)]

length(features)
[1] 28

We have length(features) features.

19.1.3 test sampling function

sample_features <- sample(features, 4, replace = FALSE)

curent_formula <- paste0( target ,' ~ ', paste0(sample_features, collapse = " + "))

as.formula(curent_formula)
lbxglu ~ dmdeduc2.3 + dmdmartl.6 + indhhin2.11 + dmdeduc2.2

19.2 make_model_order_num

This function will return a formula with a provided number of selected features selected at random

make_model_order_num <- function(num_features){
  
  set.seed(NULL)
  
  sample_features <- sample(features, num_features, replace = FALSE)

  curent_formula <- paste0(target,  ' ~ ', paste0(sample_features, collapse = " + "))

return(as.formula(curent_formula))
}

19.2.1 test

make_model_order_num(3)
lbxglu ~ dmdmartl.6 + riagendr.2 + ridreth1.3
<environment: 0x000002322dc04bc8>
make_model_order_num(3)
lbxglu ~ dmdmartl.4 + dmdeduc2.4 + indhhin2.8
<environment: 0x00000232319605b8>
make_model_order_num(6)
lbxglu ~ ridreth1.5 + indhhin2.2 + diq010.2 + dmdeduc2.5 + ridreth1.2 + 
    indhhin2.6
<environment: 0x0000023231f57fd0>

19.3 df_model

This is a dataframe to hold the model options

df_model <- tribble(
    ~model_name, ~model_creator, ~model_id,
#    "zero", make_model(0)
    "Fold1", make_model_order_num(1), 1,
    "Fold2", make_model_order_num(2), 2,
    "Fold3", make_model_order_num(3), 3,
    "Fold4", make_model_order_num(4), 4,
    "Fold5",  make_model_order_num(5), 5,
    "Fold6" , make_model_order_num(6), 6,
    "Fold7", make_model_order_num(7), 7,
    "Fold8", make_model_order_num(8), 8,
  )

df_model
# A tibble: 8 × 3
  model_name model_creator model_id
  <chr>      <list>           <dbl>
1 Fold1      <formula>            1
2 Fold2      <formula>            2
3 Fold3      <formula>            3
4 Fold4      <formula>            4
5 Fold5      <formula>            5
6 Fold6      <formula>            6
7 Fold7      <formula>            7
8 Fold8      <formula>            8
map(df_model,4)$model_creator
lbxglu ~ ridreth1.5 + indhhin2.14 + dmdeduc2.2 + ridreth1.3
<environment: 0x0000023226b7eed0>

\(~\)

\(~\)

19.4 Split data

library(rsample)

train_test <- initial_split(df_dV, prop = .6)
TRAIN <- training(train_test)
TEST <- testing(train_test)

TRAIN.v_fold <- vfold_cv(TRAIN, v = 8, 
                         repeats = 321)

glimpse(TRAIN.v_fold)
Rows: 2,568
Columns: 3
$ splits <list> [<vfold_split[984 x 141 x 1125 x 29]>], [<vfold_split[984 x 14…
$ id     <chr> "Repeat001", "Repeat001", "Repeat001", "Repeat001", "Repeat001"…
$ id2    <chr> "Fold1", "Fold2", "Fold3", "Fold4", "Fold5", "Fold6", "Fold7", …
TRAIN.v_fold %>% select(id2) %>% distinct()
# A tibble: 8 × 1
  id2  
  <chr>
1 Fold1
2 Fold2
3 Fold3
4 Fold4
5 Fold5
6 Fold6
7 Fold7
8 Fold8

19.4.1 Let’s Take a look at the 6th fold

TRAIN.v_fold %>%
  filter(id2=='Fold6') %>%
  glimpse()
Rows: 321
Columns: 3
$ splits <list> [<vfold_split[985 x 140 x 1125 x 29]>], [<vfold_split[985 x 14…
$ id     <chr> "Repeat001", "Repeat002", "Repeat003", "Repeat004", "Repeat005"…
$ id2    <chr> "Fold6", "Fold6", "Fold6", "Fold6", "Fold6", "Fold6", "Fold6", …

19.4.1.1 This is the TRAINing data from the 56th sample of the 6th Fold

TRAIN.56.6 <- (TRAIN.v_fold %>%
  filter(id2=='Fold6'))$splits[[56]] %>% 
  analysis()

TRAIN.56.6
# A tibble: 985 × 29
   riagendr.2 ridageyr ridreth1.2 ridreth1.3 ridreth1.4 ridreth1.5 dmdeduc2.2
        <dbl>    <dbl>      <dbl>      <dbl>      <dbl>      <dbl>      <dbl>
 1          0   -0.882          0          1          0          0          0
 2          0    1.66           0          1          0          0          1
 3          1    0.271          0          1          0          0          0
 4          1    0.502          0          0          0          0          0
 5          0    0.790          0          0          0          0          0
 6          1    1.71           0          1          0          0          0
 7          0   -0.882          0          0          1          0          1
 8          0    1.37           0          1          0          0          0
 9          1    0.675          0          0          0          0          1
10          1   -0.766          0          1          0          0          0
# ℹ 975 more rows
# ℹ 22 more variables: dmdeduc2.3 <dbl>, dmdeduc2.4 <dbl>, dmdeduc2.5 <dbl>,
#   dmdmartl.2 <dbl>, dmdmartl.3 <dbl>, dmdmartl.4 <dbl>, dmdmartl.5 <dbl>,
#   dmdmartl.6 <dbl>, indhhin2.2 <dbl>, indhhin2.3 <dbl>, indhhin2.4 <dbl>,
#   indhhin2.5 <dbl>, indhhin2.6 <dbl>, indhhin2.8 <dbl>, indhhin2.10 <dbl>,
#   indhhin2.11 <dbl>, indhhin2.12 <dbl>, indhhin2.13 <dbl>, indhhin2.14 <dbl>,
#   bmxbmi <dbl>, diq010.2 <dbl>, lbxglu <dbl>

19.4.1.2 Closer look at the relationship between R2 and RMSE

lm.TRAIN.56.6 <- lm(curent_formula , TRAIN.56.6)

TRAIN.56.6$estimate <- predict(lm.TRAIN.56.6 , TRAIN.56.6)
19.4.1.2.1 Compute R2 and RMSE :
RMSE.TRAIN.56.6 <- yardstick::rmse(TRAIN.56.6,
                                   truth = lbxglu, estimate)$.estimate


RMSE.TRAIN.56.6
[1] 1.035591
R2.TRAIN.56.6 <- yardstick::rsq(TRAIN.56.6,
                                   truth = lbxglu, estimate)$.estimate

R2.TRAIN.56.6
[1] 0.005539816
19.4.1.2.1.1 Compute SS_tot :
mean_lbx_glu <- mean(TRAIN.56.6$lbxglu)

# compute SS_tot :

(TRAIN.56.6 %>%
  mutate(e = lbxglu - mean_lbx_glu) %>%
  mutate(e2 = e^2 ) %>%
  summarise(SS_tot = sum(e2)))$SS_tot -> SS_tot

SS_tot
[1] 1062.246
19.4.1.2.2 Claim that this R2_by_formula will be pretty close to R2.TRAIN.56.6 
RMSE_to_R2 <- function(RMSE, n_rows, SS_tot){
  1 - ( (RMSE^2 * n_rows) /  SS_tot )
}

R2_by_formula <- RMSE_to_R2(RMSE.TRAIN.56.6 , nrow(TRAIN.56.6) , (SS_tot))
R2_by_formula
[1] 0.005539816
19.4.1.2.3 We’re off by:
sprintf("%.50f", R2.TRAIN.56.6 - R2_by_formula)
[1] "0.00000000000000018127860323957634136604610830545425"

19.4.2 This is the TESTing data from the 56th sample of the 6th Fold

TEST.56.6 <- (TRAIN.v_fold %>%
  filter(id2=='Fold6'))$splits[[56]] %>% 
  assessment()

TEST.56.6
# A tibble: 140 × 29
   riagendr.2 ridageyr ridreth1.2 ridreth1.3 ridreth1.4 ridreth1.5 dmdeduc2.2
        <dbl>    <dbl>      <dbl>      <dbl>      <dbl>      <dbl>      <dbl>
 1          0   -0.593          1          0          0          0          0
 2          1    0.444          0          1          0          0          0
 3          0    1.25           0          1          0          0          0
 4          0    1.54           0          1          0          0          0
 5          0   -1.34           0          0          1          0          0
 6          1   -1.69           0          1          0          0          0
 7          0    0.560          0          0          1          0          0
 8          1    1.71           0          1          0          0          0
 9          1    1.19           0          0          0          0          0
10          1   -0.824          0          0          0          1          0
# ℹ 130 more rows
# ℹ 22 more variables: dmdeduc2.3 <dbl>, dmdeduc2.4 <dbl>, dmdeduc2.5 <dbl>,
#   dmdmartl.2 <dbl>, dmdmartl.3 <dbl>, dmdmartl.4 <dbl>, dmdmartl.5 <dbl>,
#   dmdmartl.6 <dbl>, indhhin2.2 <dbl>, indhhin2.3 <dbl>, indhhin2.4 <dbl>,
#   indhhin2.5 <dbl>, indhhin2.6 <dbl>, indhhin2.8 <dbl>, indhhin2.10 <dbl>,
#   indhhin2.11 <dbl>, indhhin2.12 <dbl>, indhhin2.13 <dbl>, indhhin2.14 <dbl>,
#   bmxbmi <dbl>, diq010.2 <dbl>, lbxglu <dbl>

\(~\)

\(~\)

19.5 Join df_model to folds

We’re joining the model tuning grid to the folds

glimpse(TRAIN.v_fold)
Rows: 2,568
Columns: 3
$ splits <list> [<vfold_split[984 x 141 x 1125 x 29]>], [<vfold_split[984 x 14…
$ id     <chr> "Repeat001", "Repeat001", "Repeat001", "Repeat001", "Repeat001"…
$ id2    <chr> "Fold1", "Fold2", "Fold3", "Fold4", "Fold5", "Fold6", "Fold7", …
glimpse(df_model)
Rows: 8
Columns: 3
$ model_name    <chr> "Fold1", "Fold2", "Fold3", "Fold4", "Fold5", "Fold6", "F…
$ model_creator <list> <lbxglu ~ ridreth1.4>, <lbxglu ~ indhhin2.14 + ridageyr…
$ model_id      <dbl> 1, 2, 3, 4, 5, 6, 7, 8
df_model <- TRAIN.v_fold %>% 
  left_join(df_model, by = c('id2'="model_name")) 

glimpse(df_model)
Rows: 2,568
Columns: 5
$ splits        <list> [<vfold_split[984 x 141 x 1125 x 29]>], [<vfold_split[9…
$ id            <chr> "Repeat001", "Repeat001", "Repeat001", "Repeat001", "Rep…
$ id2           <chr> "Fold1", "Fold2", "Fold3", "Fold4", "Fold5", "Fold6", "F…
$ model_creator <list> <lbxglu ~ ridreth1.4>, <lbxglu ~ indhhin2.14 + ridageyr…
$ model_id      <dbl> 1, 2, 3, 4, 5, 6, 7, 8, 1, 2, 3, 4, 5, 6, 7, 8, 1, 2, 3,…

\(~\)

\(~\)

19.6 Adjusted R2

The lm_model function below will take in:

  • an rsample::analysis data set from the sample
  • a formula that we will pass in later with ...:

From those inputs it is instructed to only return Adjusted R2 which is a numerical value.

lm_model <- function(data, ...){
  
  LM <- lm(... , analysis(data))
  R2 <- summary(LM)$adj.r.squared 
  return(R2)
}

19.6.1 Test function:

curent_formula
[1] "lbxglu ~ dmdeduc2.3 + dmdmartl.6 + indhhin2.11 + dmdeduc2.2"
Adj_R2.TRAIN.56.6 <- lm_model((TRAIN.v_fold %>%
  filter(id2=='Fold6'))$splits[[56]] , curent_formula)

Adj_R2.TRAIN.56.6 == summary(lm.TRAIN.56.6)$adj.r.squared
[1] TRUE

19.6.1.1 Confirm with above:

est_Adj_r2 <- function(r2_est,
                       num_features,
                       size_data){
  X <- 1 - r2_est
  Y <- size_data -1
  Z <- size_data - num_features -1 
  
  S <- 1 - (X)*(Y/Z)
  return(S)
  }

num_features_TRAIN.56.6 <- str_count(curent_formula," [./+] ") + 1


est_Adj_r2(R2.TRAIN.56.6, num_features_TRAIN.56.6, nrow(TRAIN.56.6))
[1] 0.001480795

19.6.1.2 We’re off by:

sprintf("%.50f", Adj_R2.TRAIN.56.6 - est_Adj_r2(R2.TRAIN.56.6, num_features_TRAIN.56.6, nrow(TRAIN.56.6)))
[1] "0.00000000000000000000000000000000000000000000000000"

19.7 Get Estimates

The purrr library in R is mysterious and powerful; here, map2_dbl is going to look to return a numeric value, a double from the computation.

If you run ?map2_dbl it will display:

map2_dbl(.x, .y, .f, ...)

In the context of our current status:

  • df_model$spilts gives us a list of data - .x
  • df_model$model_creator gives us a formula - .y
  • lm_model is a function .f
    • this function takes in two values data and ...
  • The value it will return from us will be the Adj_R2 from lm_model

We will now run all the models and store the results in Adj_R2:

toc <- Sys.time()

df_model$Adj_R2 <- map2_dbl(
  df_model$splits,
  df_model$model_creator,
  lm_model
)

tic <- Sys.time()

print(paste0("Adj R2 estimates in ", round(tic - toc , 4 ) , " seconds " ))
[1] "Adj R2 estimates in 2.9966 seconds "

We just ran a bunch of models and computed R2 for each of them!:

glimpse(df_model)
Rows: 2,568
Columns: 6
$ splits        <list> [<vfold_split[984 x 141 x 1125 x 29]>], [<vfold_split[9…
$ id            <chr> "Repeat001", "Repeat001", "Repeat001", "Repeat001", "Rep…
$ id2           <chr> "Fold1", "Fold2", "Fold3", "Fold4", "Fold5", "Fold6", "F…
$ model_creator <list> <lbxglu ~ ridreth1.4>, <lbxglu ~ indhhin2.14 + ridageyr…
$ model_id      <dbl> 1, 2, 3, 4, 5, 6, 7, 8, 1, 2, 3, 4, 5, 6, 7, 8, 1, 2, 3,…
$ Adj_R2        <dbl> -0.0006628054, 0.0540125975, 0.2954475893, 0.0152728369,…

19.7.1 Display Results

df_model %>%
  ggplot(aes(x=id, 
         y=Adj_R2,
         fill = Adj_R2)) +
  geom_bar(stat = 'identity') +
  scale_fill_gradient(low = "yellow", high = "red", na.value = NA) +
  coord_flip() +
  facet_wrap( ~ model_id)

\(~\)

\(~\)

19.8 RMSE

To compute RMSE we need to know how the model performs it’s holdout set:

holdout_results <- function(splits, ...) {
  
  mod <- lm(..., data = analysis(splits))
  
  holdout <- assessment(splits)
  
  holdout$estimate <- predict(mod,holdout)
  
  yardstick::rmse(holdout,
                     truth=lbxglu, estimate)$.estimate
}

19.8.1 Compute Errors

toc <- Sys.time()

df_model$RMSE <- map2_dbl(
  df_model$splits,
  df_model$model_creator,
  holdout_results
)

tic <- Sys.time()

print(paste0("RMSE estimates in ", round(tic - toc , 4 ) , " seconds " ))
[1] "RMSE estimates in 8.3397 seconds "

\(~\)

\(~\)

19.9 Compare Results

glimpse(df_model)
Rows: 2,568
Columns: 7
$ splits        <list> [<vfold_split[984 x 141 x 1125 x 29]>], [<vfold_split[9…
$ id            <chr> "Repeat001", "Repeat001", "Repeat001", "Repeat001", "Rep…
$ id2           <chr> "Fold1", "Fold2", "Fold3", "Fold4", "Fold5", "Fold6", "F…
$ model_creator <list> <lbxglu ~ ridreth1.4>, <lbxglu ~ indhhin2.14 + ridageyr…
$ model_id      <dbl> 1, 2, 3, 4, 5, 6, 7, 8, 1, 2, 3, 4, 5, 6, 7, 8, 1, 2, 3,…
$ Adj_R2        <dbl> -0.0006628054, 0.0540125975, 0.2954475893, 0.0152728369,…
$ RMSE          <dbl> 0.9643907, 0.7680053, 0.7646919, 0.8023085, 1.1719544, 0…

19.9.1 Graphs

While we see that models with higher number of features have larger Adjusted R2 There appears to be little correlation between Adjusted R2 and model performance:

df_model %>%
  ggplot(aes(x=Adj_R2,
             y=RMSE,
             color=id)) +
  geom_point() +
  facet_wrap(~model_id) + 
  theme(legend.position = "none")

# Normalize RMSE and R2 , remove outliers 
COR <-df_model %>%
  mutate_at(vars(Adj_R2,RMSE),scale) %>%
  filter(abs(Adj_R2) <2 ) %>%
  filter(abs(RMSE) <2 )
Warning: Using one column matrices in `filter()` was deprecated in dplyr 1.1.0.
ℹ Please use one dimensional logical vectors instead.
COR %>%
  ggplot(aes(x=Adj_R2,
             y=RMSE,
             color=id)) +
  geom_point() +
  facet_wrap(~model_id) + 
  theme(legend.position = "none")

COR %>%
  ggplot(aes(x=Adj_R2,
             y=RMSE,
             color=id,
             shape = as.factor(model_id))) +
  geom_point() +
  scale_shape_manual(values=seq(0:8)) + 
  theme(legend.position = "none")

COR %>%
  ggplot(aes(x=Adj_R2,
             y=RMSE,
             color=as.factor(model_id))
         ) +
  geom_point()

COR %>%
  filter(Adj_R2 > 1) %>%
  ggplot(aes(x=Adj_R2,
             y=RMSE,
             color=as.factor(model_id))
         ) +
  geom_point()

cor.test(COR$Adj_R2, COR$RMSE, method=c("pearson"))

    Pearson's product-moment correlation

data:  COR$Adj_R2 and COR$RMSE
t = -15.079, df = 2467, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 -0.3262034 -0.2539555
sample estimates:
       cor 
-0.2904934 
t.test(COR$Adj_R2, COR$RMSE,paired=TRUE)

    Paired t-test

data:  COR$Adj_R2 and COR$RMSE
t = 2.5703, df = 2468, p-value = 0.01022
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
 0.01875407 0.13944690
sample estimates:
mean difference 
     0.07910049

19.10 “Expected Distributions” :

What might the relationship between RMSE and Adjusted R2 look like:

Random_RMSEs <- runif(100000 , min = 1 , max = 25*100000)

R2.Random_RMSEs <- map_dbl(Random_RMSEs, RMSE_to_R2 , nrow(TRAIN.56.6) , SS_tot)

Adj_R2.Random_RMSEs <- map_dbl(R2.Random_RMSEs,
        est_Adj_r2,
        num_features_TRAIN.56.6,
        nrow(TRAIN.56.6))

Randm_compare <- tibble(Random_RMSEs, Adj_R2.Random_RMSEs)

Randm_compare %>%
  ggplot(aes(x=Adj_R2.Random_RMSEs, y=Random_RMSEs)) +
  geom_point()

Randm_compare %>%
  mutate_at(vars(Adj_R2.Random_RMSEs,Random_RMSEs), scale) %>%
  ggplot(aes(x=Adj_R2.Random_RMSEs, y=Random_RMSEs)) +
  geom_point()

19.11 “Expected Distributions” with transformations -

19.11.1 if N changes shouldn’t SS_tot also change :

RMSE_to_Adj_R2 <- function(RMSE, n_rows, SS_tot, n_features ){
  R2 <- RMSE_to_R2(RMSE, n_rows, SS_tot)
  Adj_R2 <- est_Adj_r2(R2, n_features , n_rows)
  return(Adj_R2)
}
Adj_R2.double_rows <- map_dbl(Random_RMSEs, 
                              RMSE_to_Adj_R2 , 
                              nrow(TRAIN.56.6)*2 , 
                              SS_tot = SS_tot, 
                              n_features = num_features_TRAIN.56.6)

Randm_compare.Adj_R2.double_rows <- tibble(Random_RMSEs, 
                                           Adj_R2.double_rows)

Adj_R2.tripple_ss_tot <- map_dbl(Random_RMSEs, 
                                RMSE_to_Adj_R2 , 
                                nrow(TRAIN.56.6) , 
                                SS_tot = SS_tot*3, 
                                n_features = num_features_TRAIN.56.6)

Randm_compare.Adj_R2.tripple_ss_tot <- tibble(Random_RMSEs, 
                                              Adj_R2.tripple_ss_tot)

Adj_R2.double_rows_tripple_ss_tot <- map_dbl(Random_RMSEs, 
                                             RMSE_to_Adj_R2 , 
                                             nrow(TRAIN.56.6)*2 , 
                                             SS_tot = SS_tot*3, 
                                             n_features = num_features_TRAIN.56.6)

Randm_compare.Adj_R2.double_rows_tripple_ss_tot <- tibble(Random_RMSEs,
                                                           Adj_R2.double_rows_tripple_ss_tot,
                                                           )

19.11.2 Double Features

Each of those might have a variation on the number of features :

Adj_R2.double_rows.double_features <- map_dbl(Random_RMSEs, 
                              RMSE_to_Adj_R2 , 
                              nrow(TRAIN.56.6)*2 , 
                              SS_tot = SS_tot, 
                              n_features = num_features_TRAIN.56.6*2)

Randm_compare.Adj_R2.double_rows.double_features <- tibble(Random_RMSEs, 
                                           Adj_R2.double_rows.double_features)

Adj_R2.tripple_ss_tot.double_features <- map_dbl(Random_RMSEs, 
                                RMSE_to_Adj_R2 , 
                                nrow(TRAIN.56.6) , 
                                SS_tot = SS_tot*3, 
                                n_features = num_features_TRAIN.56.6*2)

Randm_compare.Adj_R2.tripple_ss_tot.double_feature <- tibble(Random_RMSEs, 
                                              Adj_R2.tripple_ss_tot.double_features)

Adj_R2.double_rows_tripple_ss_tot.double_features <- map_dbl(Random_RMSEs, 
                                             RMSE_to_Adj_R2 , 
                                             nrow(TRAIN.56.6)*2 , 
                                             SS_tot = SS_tot*3, 
                                             n_features = num_features_TRAIN.56.6*2)

Randm_compare.Adj_R2.double_rows_tripple_ss_tot.double_features <- tibble(Random_RMSEs,
                                                           Adj_R2.double_rows_tripple_ss_tot.double_features,
                                                           )
compare_round2 <- Randm_compare %>%
  left_join(Randm_compare.Adj_R2.double_rows) %>%
  left_join(Randm_compare.Adj_R2.tripple_ss_tot) %>%
  left_join(Randm_compare.Adj_R2.double_rows_tripple_ss_tot) %>%
  left_join(Randm_compare.Adj_R2.double_rows.double_features) %>%
  left_join(Randm_compare.Adj_R2.tripple_ss_tot.double_feature) %>%
  left_join(Randm_compare.Adj_R2.double_rows_tripple_ss_tot.double_features)
Joining with `by = join_by(Random_RMSEs)`
Warning in left_join(., Randm_compare.Adj_R2.double_rows): Detected an unexpected many-to-many relationship between `x` and `y`.
ℹ Row 55307 of `x` matches multiple rows in `y`.
ℹ Row 55307 of `y` matches multiple rows in `x`.
ℹ If a many-to-many relationship is expected, set `relationship =
  "many-to-many"` to silence this warning.
Joining with `by = join_by(Random_RMSEs)`
Warning in left_join(., Randm_compare.Adj_R2.tripple_ss_tot): Detected an unexpected many-to-many relationship between `x` and `y`.
ℹ Row 55307 of `x` matches multiple rows in `y`.
ℹ Row 55307 of `y` matches multiple rows in `x`.
ℹ If a many-to-many relationship is expected, set `relationship =
  "many-to-many"` to silence this warning.
Joining with `by = join_by(Random_RMSEs)`
Warning in left_join(., Randm_compare.Adj_R2.double_rows_tripple_ss_tot): Detected an unexpected many-to-many relationship between `x` and `y`.
ℹ Row 55307 of `x` matches multiple rows in `y`.
ℹ Row 55307 of `y` matches multiple rows in `x`.
ℹ If a many-to-many relationship is expected, set `relationship =
  "many-to-many"` to silence this warning.
Joining with `by = join_by(Random_RMSEs)`
Warning in left_join(., Randm_compare.Adj_R2.double_rows.double_features): Detected an unexpected many-to-many relationship between `x` and `y`.
ℹ Row 55307 of `x` matches multiple rows in `y`.
ℹ Row 55307 of `y` matches multiple rows in `x`.
ℹ If a many-to-many relationship is expected, set `relationship =
  "many-to-many"` to silence this warning.
Joining with `by = join_by(Random_RMSEs)`
Warning in left_join(., Randm_compare.Adj_R2.tripple_ss_tot.double_feature): Detected an unexpected many-to-many relationship between `x` and `y`.
ℹ Row 55307 of `x` matches multiple rows in `y`.
ℹ Row 55307 of `y` matches multiple rows in `x`.
ℹ If a many-to-many relationship is expected, set `relationship =
  "many-to-many"` to silence this warning.
Joining with `by = join_by(Random_RMSEs)`
Warning in left_join(., Randm_compare.Adj_R2.double_rows_tripple_ss_tot.double_features): Detected an unexpected many-to-many relationship between `x` and `y`.
ℹ Row 55307 of `x` matches multiple rows in `y`.
ℹ Row 55307 of `y` matches multiple rows in `x`.
ℹ If a many-to-many relationship is expected, set `relationship =
  "many-to-many"` to silence this warning.
compare_round2 %>%
  pivot_longer(!Random_RMSEs, 
               names_to = "transformation",
               values_to = "Adj_R2"
  ) -> compare_joins.long2

glimpse(compare_joins.long2)
Rows: 700,882
Columns: 3
$ Random_RMSEs   <dbl> 1180567.7, 1180567.7, 1180567.7, 1180567.7, 1180567.7, …
$ transformation <chr> "Adj_R2.Random_RMSEs", "Adj_R2.double_rows", "Adj_R2.tr…
$ Adj_R2         <dbl> -1.297663e+12, -2.590038e+12, -4.325543e+11, -8.633459e…

19.12 Graphs

compare_joins.long2 %>%
  ggplot(aes(x= Adj_R2,
             y=Random_RMSEs,
             color = transformation )) +
  geom_point() + 
  facet_wrap(~transformation)

compare_joins.long2 %>%
  ggplot(aes(x= Adj_R2,
             y=Random_RMSEs,
             color = transformation )) +
  geom_point()

19.13 RMSE has multiple values of Adjusted R2

When you take into account the other factors that goes into computing it - the same RMSE-value could be any number of Adjusted R2 values:

compare_joins.long2 %>%
  ggplot(aes(x=  Random_RMSEs ,
             y=  Adj_R2 ,
             color = transformation )) +
  geom_point()

19.14 Simulating what we’re seeing:

19.14.1 Now each of our RMSEs will be randomly assigned to one Adjusted R2 value

glimpse(compare_joins.long2)
Rows: 700,882
Columns: 3
$ Random_RMSEs   <dbl> 1180567.7, 1180567.7, 1180567.7, 1180567.7, 1180567.7, …
$ transformation <chr> "Adj_R2.Random_RMSEs", "Adj_R2.double_rows", "Adj_R2.tr…
$ Adj_R2         <dbl> -1.297663e+12, -2.590038e+12, -4.325543e+11, -8.633459e…
compare_joins.long2 %>%
  select(transformation) %>%
  distinct()
# A tibble: 7 × 1
  transformation                                   
  <chr>                                            
1 Adj_R2.Random_RMSEs                              
2 Adj_R2.double_rows                               
3 Adj_R2.tripple_ss_tot                            
4 Adj_R2.double_rows_tripple_ss_tot                
5 Adj_R2.double_rows.double_features               
6 Adj_R2.tripple_ss_tot.double_features            
7 Adj_R2.double_rows_tripple_ss_tot.double_features
compare_joins.long2 %>%
  group_by(transformation) %>%
  summarise(mean_adj_r2 = mean(Adj_R2))
# A tibble: 7 × 2
  transformation                                    mean_adj_r2
  <chr>                                                   <dbl>
1 Adj_R2.Random_RMSEs                                  -1.93e12
2 Adj_R2.double_rows                                   -3.86e12
3 Adj_R2.double_rows.double_features                   -3.87e12
4 Adj_R2.double_rows_tripple_ss_tot                    -1.29e12
5 Adj_R2.double_rows_tripple_ss_tot.double_features    -1.29e12
6 Adj_R2.tripple_ss_tot                                -6.44e11
7 Adj_R2.tripple_ss_tot.double_features                -6.47e11

19.14.1.1 We can remove the correlated Adj_R2s to get a better sense of what might be going on :

compare_joins.long2.filter <- compare_joins.long2 %>%
  filter(transformation %in% c('Adj_R2.Random_RMSEs',
                               'Adj_R2.double_rows.double_features',
                               'Adj_R2.double_rows_tripple_ss_tot',
                               'Adj_R2.tripple_ss_tot')
         )

19.14.1.2 For each of the RMSE we will randomly assign an Adjusted R2 

rand_sort <- runif(nrow(compare_joins.long2.filter))
glimpse(rand_sort)
 num [1:400504] 0.606 0.261 0.13 0.637 0.801 ...
compare_joins.long3 <- cbind(compare_joins.long2.filter, rand_sort)
glimpse(compare_joins.long3)
Rows: 400,504
Columns: 4
$ Random_RMSEs   <dbl> 1180567.7, 1180567.7, 1180567.7, 1180567.7, 1513745.9, …
$ transformation <chr> "Adj_R2.Random_RMSEs", "Adj_R2.tripple_ss_tot", "Adj_R2…
$ Adj_R2         <dbl> -1.297663e+12, -4.325543e+11, -8.633459e+11, -2.595321e…
$ rand_sort      <dbl> 0.60635543, 0.26092583, 0.13011574, 0.63667996, 0.80121…
compare_joins.long4 <- compare_joins.long3 %>%
  arrange(rand_sort) %>%
  group_by(Random_RMSEs) %>%
  mutate(rn = row_number()) %>%
  filter(rn == 1) %>%
  ungroup() %>%
  select(-rn)


compare_joins.long4
# A tibble: 99,999 × 4
   Random_RMSEs transformation                       Adj_R2   rand_sort
          <dbl> <chr>                                 <dbl>       <dbl>
 1      477623. Adj_R2.double_rows.double_features -4.25e11 0.000000796
 2     1658287. Adj_R2.double_rows_tripple_ss_tot  -1.70e12 0.00000246 
 3      133165. Adj_R2.Random_RMSEs                -1.65e10 0.00000746 
 4      751551. Adj_R2.double_rows_tripple_ss_tot  -3.50e11 0.00000906 
 5      228569. Adj_R2.tripple_ss_tot              -1.62e10 0.0000114  
 6     1080655. Adj_R2.double_rows_tripple_ss_tot  -7.23e11 0.0000116  
 7       83254. Adj_R2.double_rows_tripple_ss_tot  -4.29e 9 0.0000187  
 8     2055233. Adj_R2.double_rows_tripple_ss_tot  -2.62e12 0.0000220  
 9      255537. Adj_R2.double_rows.double_features -1.22e11 0.0000229  
10     1043269. Adj_R2.Random_RMSEs                -1.01e12 0.0000229  
# ℹ 99,989 more rows

19.15 Graphs

And we’ll sample some of the RMSE at random too:

compare_joins.long4 %>%
  mutate_at(vars(Adj_R2,Random_RMSEs), scale) %>%
  filter(rand_sort > .90 ) %>%
  ggplot(aes(x=   Adj_R2 ,
             y=   Random_RMSEs,
             color = as.factor(transformation))) +
  geom_point() +
  theme(legend.position = "none")

Distribution is very difficult to tell even with colored points - keep in mind that each RMSE is getting associated with a different Adjusted R2 value for each different fold and repeat as they each have different N and number of features.

20 Top 5 Formulas

20.1 RMSE

(df_model %>%
  arrange(RMSE) %>%
  filter(row_number() < 5))$RMSE
[1] 0.4264912 0.4285924 0.4337156 0.4674212
Top_5_RMSE_formulas <- (df_model %>%
  arrange(RMSE) %>%
  filter(row_number() < 5))$model_creator

Top_5_RMSE_formulas
[[1]]
lbxglu ~ diq010.2 + ridreth1.2 + dmdeduc2.4
<environment: 0x0000023226b87b50>

[[2]]
lbxglu ~ ridreth1.3 + indhhin2.11 + indhhin2.2 + diq010.2 + ridreth1.2 + 
    bmxbmi + dmdmartl.4
<environment: 0x0000023226b5dc00>

[[3]]
lbxglu ~ diq010.2 + ridreth1.2 + dmdeduc2.4
<environment: 0x0000023226b87b50>

[[4]]
lbxglu ~ diq010.2 + ridreth1.2 + dmdeduc2.4
<environment: 0x0000023226b87b50>

20.2 Adj_R2

(df_model %>%
  arrange(-Adj_R2) %>%
  filter(row_number() < 5))$Adj_R2
[1] 0.3574102 0.3546240 0.3499443 0.3496318
Top_5_AdjR2_formulas <- (df_model %>%
  arrange(-Adj_R2) %>%
  filter(row_number() < 5))$model_creator

Top_5_AdjR2_formulas
[[1]]
lbxglu ~ ridreth1.3 + indhhin2.11 + indhhin2.2 + diq010.2 + ridreth1.2 + 
    bmxbmi + dmdmartl.4
<environment: 0x0000023226b5dc00>

[[2]]
lbxglu ~ dmdeduc2.2 + diq010.2 + ridreth1.2 + dmdeduc2.3 + dmdmartl.3 + 
    dmdmartl.4 + indhhin2.8 + indhhin2.2
<environment: 0x0000023226b53ae8>

[[3]]
lbxglu ~ ridreth1.3 + indhhin2.11 + indhhin2.2 + diq010.2 + ridreth1.2 + 
    bmxbmi + dmdmartl.4
<environment: 0x0000023226b5dc00>

[[4]]
lbxglu ~ ridreth1.3 + indhhin2.11 + indhhin2.2 + diq010.2 + ridreth1.2 + 
    bmxbmi + dmdmartl.4
<environment: 0x0000023226b5dc00>

21 Clash of the Titians

Best_RMSE_formula <- Top_5_RMSE_formulas[[1]] 
Best_AdjR2_formula <- Top_5_AdjR2_formulas[[1]]


if(Best_RMSE_formula == Best_AdjR2_formula){
  Best_RMSE_formula <- Top_5_RMSE_formulas[[1]] 
  Best_AdjR2_formula <- Top_5_AdjR2_formulas[[2]]
}

Best_RMSE_formula VS Best_AdjR2_formula

Final.Glm_function <- function(formula, data){
  lm(formula, data)
}

21.1 Train the models:

Final.Glm.Adj_R2 <- Final.Glm_function(Best_AdjR2_formula , TRAIN)
Final.Glm.RMSE <- Final.Glm_function(Best_RMSE_formula, TRAIN)

21.2 Compare model performace:

TEST.scored <- TEST

TEST.scored$estimate <- predict(Final.Glm.Adj_R2, TEST) 

TEST.Adj_R2 <- TEST.scored %>%
  mutate(model = "Adj_R2")

TEST.scored$estimate <- predict(Final.Glm.RMSE, TEST) 

TEST.RMSE <- TEST.scored %>%
  mutate(model = "RMSE")

TEST_stacked <- bind_rows(TEST.Adj_R2, TEST.RMSE)
TEST_stacked %>%
  group_by(model) %>%
  yardstick::rmse(truth=lbxglu, estimate)
# A tibble: 2 × 4
  model  .metric .estimator .estimate
  <chr>  <chr>   <chr>          <dbl>
1 Adj_R2 rmse    standard       0.819
2 RMSE   rmse    standard       0.816
TEST_stacked %>%
  group_by(model) %>%
  mutate(error = estimate - lbxglu) %>%
  arrange(error) %>%
  mutate(order_n = row_number()) %>%
  ggplot(aes(x=order_n, 
             y=error,
             color=model)) +
  geom_point() +
  geom_line() +
  facet_wrap(~model)

TEST_stacked
# A tibble: 1,502 × 31
   riagendr.2 ridageyr ridreth1.2 ridreth1.3 ridreth1.4 ridreth1.5 dmdeduc2.2
        <dbl>    <dbl>      <dbl>      <dbl>      <dbl>      <dbl>      <dbl>
 1          1    1.25           0          0          0          0          1
 2          0   -0.305          0          0          0          1          1
 3          1    0.963          1          0          0          0          0
 4          0    0.963          0          0          1          0          0
 5          1   -1.52           0          0          0          1          0
 6          0    0.906          0          1          0          0          0
 7          1   -0.766          1          0          0          0          0
 8          1   -1.75           0          0          1          0          0
 9          0   -1.52           0          1          0          0          0
10          1   -1.75           0          0          1          0          0
# ℹ 1,492 more rows
# ℹ 24 more variables: dmdeduc2.3 <dbl>, dmdeduc2.4 <dbl>, dmdeduc2.5 <dbl>,
#   dmdmartl.2 <dbl>, dmdmartl.3 <dbl>, dmdmartl.4 <dbl>, dmdmartl.5 <dbl>,
#   dmdmartl.6 <dbl>, indhhin2.2 <dbl>, indhhin2.3 <dbl>, indhhin2.4 <dbl>,
#   indhhin2.5 <dbl>, indhhin2.6 <dbl>, indhhin2.8 <dbl>, indhhin2.10 <dbl>,
#   indhhin2.11 <dbl>, indhhin2.12 <dbl>, indhhin2.13 <dbl>, indhhin2.14 <dbl>,
#   bmxbmi <dbl>, diq010.2 <dbl>, lbxglu <dbl>, estimate <dbl>, model <chr>
TEST_stacked.RMSE.byGroup <- TEST_stacked %>%
  group_by(model, riagendr.2, ridreth1.2, dmdeduc2.2, dmdmartl.2, indhhin2.2, diq010.2) %>%
  yardstick::rmse(truth=lbxglu, estimate)   

TEST_stacked.RMSE.byGroup %>% glimpse()
Rows: 78
Columns: 10
$ model      <chr> "Adj_R2", "Adj_R2", "Adj_R2", "Adj_R2", "Adj_R2", "Adj_R2",…
$ riagendr.2 <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1,…
$ ridreth1.2 <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0,…
$ dmdeduc2.2 <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 1, 1, 1, 0,…
$ dmdmartl.2 <dbl> 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0,…
$ indhhin2.2 <dbl> 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 1, 0,…
$ diq010.2   <dbl> 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1, 0, 1, 0,…
$ .metric    <chr> "rmse", "rmse", "rmse", "rmse", "rmse", "rmse", "rmse", "rm…
$ .estimator <chr> "standard", "standard", "standard", "standard", "standard",…
$ .estimate  <dbl> 1.8463314, 0.3676297, 0.9113309, 0.2523847, 2.5158934, 0.29…
TEST_stacked.RMSE.byGroup %>%
  group_by(model) %>%
  ggplot(aes(x=riagendr.2, 
             y=.estimate,
             fill= model )) +
  geom_bar(stat='identity', position = 'dodge') +
  facet_wrap(~ridreth1.2+diq010.2)

TEST_stacked %>%
  group_by(model, riagendr.2, ridreth1.2, dmdeduc2.2, dmdmartl.2, indhhin2.2, diq010.2) %>%
  mutate(error = estimate - lbxglu) %>%
  arrange(error) %>%
  mutate(order_n = row_number()) %>%
  ggplot(aes(x=order_n, 
             y=error,
             color=model)) +
  geom_point() +
  geom_line() +
  facet_wrap(~ridreth1.2+diq010.2)

TEST_stacked %>%
  group_by(model) %>%
  yardstick::rsq(truth=lbxglu, estimate)
# A tibble: 2 × 4
  model  .metric .estimator .estimate
  <chr>  <chr>   <chr>          <dbl>
1 Adj_R2 rsq     standard       0.318
2 RMSE   rsq     standard       0.324