9 Exploratory Data Analysis at Scale

Code

Part4_Data <- here::here('DATA/Part_4')

library('kableExtra')
library('tidyverse')

── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
✔ dplyr     1.1.4     ✔ readr     2.1.5
✔ forcats   1.0.0     ✔ stringr   1.5.1
✔ ggplot2   3.5.1     ✔ tibble    3.2.1
✔ lubridate 1.9.3     ✔ tidyr     1.3.1
✔ purrr     1.0.2     
── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
✖ dplyr::filter()     masks stats::filter()
✖ dplyr::group_rows() masks kableExtra::group_rows()
✖ dplyr::lag()        masks stats::lag()
ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors

Code

A_DATA_2 <- readRDS(file.path(Part4_Data,'A_DATA_2.RDS'))

A_DATA_TBL_2.t_ks_result.furrr <- readRDS(file.path(Part4_Data,'A_DATA_TBL_2.t_ks_result.furrr.RDS'))

FEATURE_TYPE <- readRDS(file.path(Part4_Data,'FEATURE_TYPE.RDS'))

numeric_features <- FEATURE_TYPE$numeric_features
categorical_features <- FEATURE_TYPE$categorical_features

9.1 Investigate Results

We can make make our results scroll-able if we use kableExtra:

Code

A_DATA_TBL_2.t_ks_result.furrr %>%
  select(Feature, mean_diff_est , ttest.pvalue, kstest.pvalue, N_Target, mean_Target, sd_Target, N_Control, mean_Control, sd_Control) %>%
  mutate(across(where(is.numeric), round, 3))  %>%
  kableExtra::kbl() %>% # kableExtra from here down
  kable_paper() %>%
  scroll_box(width = "100%", height = "200px")

Warning: There was 1 warning in `mutate()`.
ℹ In argument: `across(where(is.numeric), round, 3)`.
Caused by warning:
! The `...` argument of `across()` is deprecated as of dplyr 1.1.0.
Supply arguments directly to `.fns` through an anonymous function instead.

  # Previously
  across(a:b, mean, na.rm = TRUE)

  # Now
  across(a:b, \(x) mean(x, na.rm = TRUE))

Feature	mean_diff_est	ttest.pvalue	kstest.pvalue	N_Target	mean_Target	sd_Target	N_Control	mean_Control	sd_Control
PHAFSTHR	0.403	0.000	0.000	2002	11.331	3.756	17227	10.928	3.542
BPXML1	15.089	0.000	0.000	6212	160.122	26.533	66292	145.032	22.621
PHAFSTMN	0.210	0.607	0.953	2002	29.980	17.260	17227	29.770	17.302
BPXDI4	0.966	0.223	0.039	665	67.738	19.806	7687	66.772	16.984
BPXPLS	-0.084	0.625	0.286	6246	74.368	13.046	66470	74.452	12.639
BPXDI1	2.029	0.000	0.000	5749	68.184	14.977	61757	66.156	14.895
BPXDI3	1.496	0.000	0.000	5740	67.521	15.235	60517	66.024	15.184
BPXDI2	1.964	0.000	0.000	5810	68.058	14.962	61041	66.094	14.996
BPXSY4	16.500	0.000	0.000	665	135.919	23.407	7687	119.419	20.331
BPXCHR	-3.384	0.519	0.817	15	96.933	19.783	15152	100.317	17.076
BPXSY3	13.999	0.000	0.000	5740	131.256	20.739	60518	117.258	18.055
Age	31.486	0.000	0.000	6807	61.527	14.780	88740	30.041	23.635
BPXSY2	14.419	0.000	0.000	5810	132.280	21.146	61041	117.860	18.455
BPXSY1	14.842	0.000	0.000	5749	133.321	21.342	61757	118.478	18.858
BPXDAR	0.835	0.069	0.016	1356	66.953	16.481	20711	66.118	14.444
BMXHEAD	NaN	NA	NA	0	NaN	NA	0	NaN	NA
LBDHDD	-5.268	0.000	0.000	4704	48.553	14.488	45568	53.821	15.288
LBDHDDSI	-0.136	0.000	0.000	4704	1.256	0.375	45568	1.392	0.395
BPXSAR	16.998	0.000	0.000	1356	134.541	22.248	20711	117.542	19.343
LBXAPB	7.345	0.000	0.001	228	101.175	28.270	2837	93.830	28.515
LBDAPBSI	0.073	0.000	0.001	228	1.012	0.283	2837	0.938	0.285
LBDLDLM	-8.538	0.000	0.000	381	100.360	38.142	2167	108.898	35.153
LBDLDMSI	-0.221	0.000	0.000	381	2.595	0.986	2167	2.816	0.909
LBDLDLN	-10.763	0.000	0.000	385	99.764	38.508	2182	110.527	35.851
LBDLDNSI	-0.278	0.000	0.000	385	2.580	0.996	2182	2.858	0.927
BMXSAD3	3.322	0.000	0.000	126	25.225	4.049	960	21.904	5.050
BMXSAD4	3.312	0.000	0.000	126	25.214	3.995	960	21.903	5.053
LBDLDL	-9.006	0.000	0.000	2180	100.390	36.569	18145	109.396	35.225
LBDLDLSI	-0.233	0.000	0.000	2180	2.596	0.946	18145	2.829	0.911
BMXSAD1	5.005	0.000	0.000	1923	25.616	4.551	18661	20.610	4.732
BMXSAD2	5.018	0.000	0.000	1923	25.612	4.570	18661	20.594	4.741
BMDAVSAD	5.005	0.000	0.000	1923	25.624	4.558	18661	20.619	4.734
BMXLEG	-1.397	0.000	0.000	5857	37.535	4.280	65870	38.932	4.238
LBXTC	-1.827	0.009	0.000	4704	181.063	46.312	45567	182.890	41.105
LBDTCSI	-0.047	0.009	0.000	4704	4.682	1.198	45567	4.730	1.063
LBXGLU	60.692	0.000	0.000	2352	160.710	68.044	18897	100.018	18.194
BMXCALF	1.379	0.000	0.000	1811	38.211	4.791	27783	36.832	5.016
BMXARML	4.123	0.000	0.000	6057	37.580	2.993	81107	33.457	6.720
BMXSUB	7.916	0.000	0.000	2175	23.325	7.689	44885	15.409	8.668
URXUCR2	-42.900	0.000	0.000	636	94.338	56.189	6600	137.238	73.324
URDUCR2S	-3792.372	0.000	0.000	636	8339.484	4967.065	6600	12131.855	6481.851
BMXTRI	4.759	0.000	0.000	2843	21.026	8.490	48206	16.267	8.204
BMXARMC	6.334	0.000	0.000	6054	34.672	5.408	81091	28.338	7.442
Poverty_Income_Ratio	-0.072	0.000	0.000	6059	2.225	1.502	80794	2.296	1.610
BMAEXLEN	22.610	0.000	0.000	450	286.258	93.019	8321	263.647	79.125
URXUCR	-11.888	0.000	0.000	4840	113.749	71.374	49920	125.637	81.455
BMXTHICR	1.186	0.000	0.000	1742	52.439	7.866	27456	51.253	8.012
LBDGLUSI	3.369	0.000	0.000	2352	8.921	3.777	18897	5.552	1.010
LBXTR	43.659	0.000	0.000	2260	157.202	159.082	18367	113.543	93.182
LBDTRSI	0.493	0.000	0.000	2260	1.775	1.796	18367	1.282	1.052
BMXRECUM	-0.479	0.912	0.944	5	89.640	9.141	7205	90.119	8.600
URXUMA2	39.630	0.000	0.000	636	55.181	209.726	6600	15.550	77.535
URDUMA2S	39.630	0.000	0.000	636	55.181	209.726	6600	15.550	77.535
BMXHIP	6.579	0.000	0.000	773	110.892	15.731	5098	104.313	14.460
URXCRS	-1050.899	0.000	0.000	4840	10055.402	6309.499	49920	11106.301	7200.588
BMXHT	10.458	0.000	0.000	6322	165.672	10.725	80726	155.214	23.879
BMXWAIST	23.277	0.000	0.000	5913	108.049	16.341	77653	84.773	21.414
PEASCTM1	149.680	0.000	0.000	4674	711.582	200.877	67355	561.902	267.205
URDACT2	88.039	0.000	0.000	636	102.720	580.014	6600	14.680	93.315
BMXWT	25.929	0.000	0.000	6306	88.116	23.925	83464	62.187	29.774
URXUMA	141.019	0.000	0.000	4840	172.300	793.228	49919	31.281	200.764
URXUMS	141.019	0.000	0.000	4840	172.300	793.228	49919	31.281	200.764
LBXIN	7.997	0.000	0.000	2284	21.110	35.946	18490	13.113	12.496
LBDINSI	47.984	0.000	0.000	2284	126.662	215.673	18490	78.678	74.976
BMXBMI	7.043	0.000	0.000	6268	31.948	7.566	80343	24.905	7.355
URDACT	141.427	0.000	0.000	3660	171.371	719.616	35584	29.944	532.255
WTSAF2YR	-19537.782	0.000	0.000	2474	61002.970	68801.008	20100	80540.753	82941.640

We can make a corresponding plot to go along with our table:

Code

plot <- A_DATA_TBL_2.t_ks_result.furrr %>%
  mutate(Feature_Prevalence_Pct = round(N_Target/(N_Target+N_Control)*100,2)) %>%
  ggplot(aes(x=round(ttest.pvalue,4) , y= round(kstest.pvalue,4), color = Feature, size = Feature_Prevalence_Pct)) +
  geom_point() + 
  theme(legend.position='none') 

plot

Warning: Removed 1 row containing missing values or values outside the scale range
(`geom_point()`).

9.2 tableby

The arsenal package also contains other helpful functions in terms of Exploratory Data Analysis:

Code

library('arsenal')


Attaching package: 'arsenal'

The following object is masked from 'package:lubridate':

    is.Date

Code

library('knitr')


A_DATA_2 %>%
  head()

# A tibble: 6 × 133
   SEQN DIABETES AGE_AT_DIAG_DM2   Age Gender Race  USAF  Birth_Country
  <dbl>    <dbl>           <dbl> <dbl> <chr>  <chr> <chr> <chr>        
1     1        0              NA     2 Female Black <NA>  USA          
2     2        0              NA    77 Male   White Yes   USA          
3     3        0              NA    10 Female White <NA>  <NA>         
4     4        0              NA     1 Male   Black <NA>  USA          
5     5        0              NA    49 Male   White Yes   USA          
6     6        0              NA    19 Female Other No    USA          
# ℹ 125 more variables: Grade_Level <chr>, Grade_Range <chr>,
#   Marital_Status <chr>, Pregnant <chr>, Household_Icome <chr>,
#   Family_Income <chr>, Poverty_Income_Ratio <dbl>, yr_range <chr>,
#   PEASCST1 <dbl>, PEASCTM1 <dbl>, PEASCCT1 <dbl>, BPXCHR <dbl>,
#   BPQ150A <dbl>, BPQ150B <dbl>, BPQ150C <dbl>, BPQ150D <dbl>, BPAARM <dbl>,
#   BPACSZ <dbl>, BPXPLS <dbl>, BPXDB <dbl>, BPXPULS <dbl>, BPXPTY <dbl>,
#   BPXML1 <dbl>, BPXSY1 <dbl>, BPXDI1 <dbl>, BPAEN1 <dbl>, BPXSY2 <dbl>, …

We can perform many of the analyses we did in the last part easily with the tableby function

Code

tableby(DIABETES_char ~ Age + Gender + Race + Marital_Status + Grade_Level + LBXGLU,
        data = A_DATA_2 %>%
          mutate(DIABETES_char = case_when(DIABETES == 1 ~ "Diabetics", 
                                   DIABETES == 0 ~ "Non-Diabetics",
                                   is.na(DIABETES) ~ "Unknown Diabetic Status"))) %>%
  summary(pfootnote=TRUE)

	Diabetics (N=6807)	Non-Diabetics (N=88740)	Unknown Diabetic Status (N=5769)	Total (N=101316)	p value
Age					< 0.001¹
Mean (SD)	61.527 (14.780)	30.041 (23.635)	11.989 (24.525)	31.128 (24.943)
Range	1.000 - 85.000	1.000 - 85.000	0.000 - 85.000	0.000 - 85.000
Gender					0.019²
Female	3371 (49.5%)	45188 (50.9%)	2864 (49.6%)	51423 (50.8%)
Male	3436 (50.5%)	43552 (49.1%)	2905 (50.4%)	49893 (49.2%)
Race					< 0.001²
Black	1823 (26.8%)	20692 (23.3%)	1129 (19.6%)	23644 (23.3%)
Mexican American	1373 (20.2%)	19426 (21.9%)	1650 (28.6%)	22449 (22.2%)
Other	611 (9.0%)	8376 (9.4%)	510 (8.8%)	9497 (9.4%)
Other Hispanic	592 (8.7%)	7201 (8.1%)	501 (8.7%)	8294 (8.2%)
White	2408 (35.4%)	33045 (37.2%)	1979 (34.3%)	37432 (36.9%)
Marital_Status					< 0.001²
N-Miss	157	35025	4620	39802
Divorced	838 (12.6%)	4599 (8.6%)	162 (14.1%)	5599 (9.1%)
Living with partner	224 (3.4%)	3892 (7.2%)	70 (6.1%)	4186 (6.8%)
Married	3634 (54.6%)	24349 (45.3%)	595 (51.8%)	28578 (46.5%)
Never married	604 (9.1%)	15531 (28.9%)	137 (11.9%)	16272 (26.5%)
Separated	253 (3.8%)	1541 (2.9%)	39 (3.4%)	1833 (3.0%)
Widowed	1097 (16.5%)	3803 (7.1%)	146 (12.7%)	5046 (8.2%)
Grade_Level					0.040²
N-Miss	6681	59497	5663	71841
10th grade	11 (8.7%)	2177 (7.4%)	9 (8.5%)	2197 (7.5%)
11th grade	12 (9.5%)	2146 (7.3%)	8 (7.5%)	2166 (7.3%)
12th grade, no diploma	0 (0.0%)	438 (1.5%)	2 (1.9%)	440 (1.5%)
1st grade	6 (4.8%)	2126 (7.3%)	2 (1.9%)	2134 (7.2%)
2nd grade	4 (3.2%)	2102 (7.2%)	1 (0.9%)	2107 (7.1%)
3rd grade	6 (4.8%)	2031 (6.9%)	6 (5.7%)	2043 (6.9%)
4th grade	6 (4.8%)	2036 (7.0%)	12 (11.3%)	2054 (7.0%)
5th grade	9 (7.1%)	2110 (7.2%)	10 (9.4%)	2129 (7.2%)
6th grade	14 (11.1%)	2219 (7.6%)	5 (4.7%)	2238 (7.6%)
7th grade	8 (6.3%)	2178 (7.4%)	11 (10.4%)	2197 (7.5%)
8th grade	11 (8.7%)	2292 (7.8%)	12 (11.3%)	2315 (7.9%)
9th grade	18 (14.3%)	2195 (7.5%)	15 (14.2%)	2228 (7.6%)
Don’t Know	0 (0.0%)	9 (0.0%)	0 (0.0%)	9 (0.0%)
GED or equivalent	0 (0.0%)	115 (0.4%)	0 (0.0%)	115 (0.4%)
High school graduate	9 (7.1%)	1422 (4.9%)	7 (6.6%)	1438 (4.9%)
Less than 5th grade	0 (0.0%)	26 (0.1%)	0 (0.0%)	26 (0.1%)
Less than 9th grade	1 (0.8%)	277 (0.9%)	1 (0.9%)	279 (0.9%)
More than high school	6 (4.8%)	980 (3.4%)	3 (2.8%)	989 (3.4%)
Never attended / kindergarten only	5 (4.0%)	2362 (8.1%)	2 (1.9%)	2369 (8.0%)
Refused	0 (0.0%)	2 (0.0%)	0 (0.0%)	2 (0.0%)
LBXGLU					< 0.001¹
N-Miss	4455	69843	5326	79624
Mean (SD)	160.710 (68.044)	100.018 (18.194)	118.363 (36.091)	106.974 (34.273)
Range	21.000 - 584.000	38.000 - 422.000	77.000 - 451.000	21.000 - 584.000

Linear Model ANOVA
Pearson’s Chi-squared test

9.3 Assessing Cohort Balance

Let’s assume there was a cohort assigned to the patient, we can take our algorithm from Section Section 7.2

Code

set.seed(8576309)

A_DATA_2$rand_class <- sample(c('Rand_A','Rand_B'), 
                            size = nrow(A_DATA_2),  
                            replace = TRUE)

A_DATA_2$rand_sort <- runif(nrow(A_DATA_2))

A_DATA_2 <- A_DATA_2 %>%
  arrange(rand_sort) %>%
  mutate(rn = row_number()) %>%
  mutate(rn_mod_5 = rn %% 5 ) %>% 
  mutate(rand_class = if_else( rn_mod_5 == 0, 
                              "Rand_C", 
                              rand_class)) %>%
  select(-rn, -rn_mod_5, -rand_sort) %>%
  mutate(rand_class = as.factor(rand_class))

We can check for balance in the cohorts among some of the features perhaps, Age, Race, and Gender with:

Code

tableby(rand_class ~ Age + Gender + Race, 
        data = A_DATA_2) %>%
  summary(pfootnote=TRUE)

	Rand_A (N=40534)	Rand_B (N=40519)	Rand_C (N=20263)	Total (N=101316)	p value
Age					0.080¹
Mean (SD)	31.336 (25.036)	30.947 (24.864)	31.075 (24.913)	31.128 (24.943)
Range	0.000 - 85.000	0.000 - 85.000	0.000 - 85.000	0.000 - 85.000
Gender					0.527²
Female	20602 (50.8%)	20484 (50.6%)	10337 (51.0%)	51423 (50.8%)
Male	19932 (49.2%)	20035 (49.4%)	9926 (49.0%)	49893 (49.2%)
Race					0.613²
Black	9464 (23.3%)	9484 (23.4%)	4696 (23.2%)	23644 (23.3%)
Mexican American	8923 (22.0%)	8988 (22.2%)	4538 (22.4%)	22449 (22.2%)
Other	3839 (9.5%)	3788 (9.3%)	1870 (9.2%)	9497 (9.4%)
Other Hispanic	3399 (8.4%)	3278 (8.1%)	1617 (8.0%)	8294 (8.2%)
White	14909 (36.8%)	14981 (37.0%)	7542 (37.2%)	37432 (36.9%)

Linear Model ANOVA
Pearson’s Chi-squared test

Above we see that both p-values of Race, and Gender are above .05 meaning the distributions of Race, and Gender appear to be random among the cohorts of rand_class; so here, the cohorts rand_class are well-balanced on Race, and Gender.

We see that the p-value of Age appears to be significant, however, the distributions appear to be similar:

Code

A_DATA_2 %>%
  ggplot(aes(x=Age, color=rand_class)) +
  geom_density()

9.4 Missing Data

Code

A_DATA_2.Num <- A_DATA_2 %>%
  select(SEQN, DIABETES, Gender, Race, Family_Income, all_of(FEATURE_TYPE$numeric_features))

The first function is the Amelia::missmap function which can be used as follows.

Code

tic <- Sys.time()

Amelia::missmap(as.data.frame(A_DATA_2.Num))

Code

toc <- Sys.time()

time.Amelia <- difftime(toc , tic , units = "secs")

Next we will review some of the functionality within the mice package:

Code

library(mice)


Attaching package: 'mice'

The following object is masked from 'package:stats':

    filter

The following objects are masked from 'package:base':

    cbind, rbind

Code

library(VIM)

Loading required package: colorspace

Loading required package: grid

VIM is ready to use.

Suggestions and bug-reports can be submitted at: https://github.com/statistikat/VIM/issues


Attaching package: 'VIM'

The following object is masked from 'package:datasets':

    sleep

Code

library(lattice)

Code

tic <- Sys.time()

#plot the missing values
plot.miss <- aggr(A_DATA_2.Num,  
     numbers=TRUE, 
     sortVars=TRUE, 
     labels=colnames(A_DATA_2.Num), 
     cex.axis=.7, 
     gap=3, 
     ylab=c("Proportion of missingness","Missingness Pattern"))

Warning in plot.aggr(res, ...): not enough vertical space to display
frequencies (too many combinations)


 Variables sorted by number of missings: 
             Variable      Count
              BMXSAD3 0.98905405
              BMXSAD4 0.98905405
              BMXHEAD 0.97536421
              LBDLDLM 0.97403174
             LBDLDMSI 0.97403174
              LBDLDLN 0.97384421
             LBDLDNSI 0.97384421
               LBXAPB 0.96934344
             LBDAPBSI 0.96934344
               BMXHIP 0.94039441
              URXUCR2 0.92734612
             URDUCR2S 0.92734612
              URXUMA2 0.92734612
             URDUMA2S 0.92734612
              URDACT2 0.92734612
               BPXDI4 0.91643965
               BPXSY4 0.91643965
             BMAEXLEN 0.90838564
             BMXRECUM 0.88619764
               BPXCHR 0.80783884
             PHAFSTHR 0.80652612
             PHAFSTMN 0.80652612
               LBDLDL 0.79523471
             LBDLDLSI 0.79523471
              BMXSAD1 0.79276718
              BMXSAD2 0.79276718
             BMDAVSAD 0.79276718
                LBXTR 0.79212563
              LBDTRSI 0.79212563
                LBXIN 0.79067472
              LBDINSI 0.79067472
               LBXGLU 0.78589759
             LBDGLUSI 0.78589759
               BPXDAR 0.78019266
               BPXSAR 0.78019266
             WTSAF2YR 0.77256307
             BMXTHICR 0.70892060
              BMXCALF 0.70493308
               URDACT 0.60521537
               BMXSUB 0.50978128
                LBXTC 0.49466027
              LBDTCSI 0.49466027
               LBDHDD 0.49465040
             LBDHDDSI 0.49465040
               BMXTRI 0.46913617
               URXUMA 0.45004738
               URXUMS 0.45004738
               URXUCR 0.45003751
               URXCRS 0.45003751
        Family_Income 0.44252635
               BPXDI3 0.33547515
               BPXSY3 0.33546528
               BPXDI2 0.32948399
               BPXSY2 0.32948399
               BPXDI1 0.32314738
               BPXSY1 0.32314738
               BMXLEG 0.28113032
               BPXML1 0.27300722
               BPXPLS 0.27083580
             PEASCTM1 0.24495637
             BMXWAIST 0.16401161
               BMXBMI 0.13341427
                BMXHT 0.12907142
              BMXARMC 0.09402266
              BMXARML 0.09381539
 Poverty_Income_Ratio 0.09076553
                BMXWT 0.06054325
             DIABETES 0.05694066
                 SEQN 0.00000000
               Gender 0.00000000
                 Race 0.00000000
                  Age 0.00000000

Code

toc <- Sys.time()

time.mice <- difftime(toc , tic , units = "secs")

Code

#Drawing margin plot
marginplot(A_DATA_2.Num[, c("Age", "BMXARML")], 
           cex.numbers = 1.2, 
           pch = 19)

Code

#Drawing margin plot
marginplot(A_DATA_2.Num[, c("Age", "BMXSAD3")], 
           cex.numbers = 1.2, 
           pch = 19)

Here’s a function to give to return the a tibble of features with percentage of non-missing values:

Code

Features_Percent_Complete <- function(data, Percent_Complete = 0){
  
  if(is.na(Percent_Complete)){Percent_Complete <- 0}   
  
  SumNa <- function(col){sum(is.na(col))}
  
  na_sums <- data %>% 
    summarise_all(SumNa) %>%
    tidyr::pivot_longer(everything() ,names_to = 'feature', values_to = 'SumNa') %>%
    arrange(-SumNa) %>%
    mutate(PctNa = SumNa/nrow(data)) %>%
    mutate(PctComp = (1 - PctNa)*100)
  
  data_out <- na_sums %>%
    filter(PctComp >= Percent_Complete)
  
return(data_out)
}

Let’s first define the features that have at least 70% data:

Code

features_all_percent_compete <- Features_Percent_Complete(A_DATA_2.Num, 0)

features_all_percent_compete

# A tibble: 72 × 4
   feature   SumNa PctNa PctComp
   <chr>     <int> <dbl>   <dbl>
 1 BMXSAD3  100207 0.989    1.09
 2 BMXSAD4  100207 0.989    1.09
 3 BMXHEAD   98820 0.975    2.46
 4 LBDLDLM   98685 0.974    2.60
 5 LBDLDMSI  98685 0.974    2.60
 6 LBDLDLN   98666 0.974    2.62
 7 LBDLDNSI  98666 0.974    2.62
 8 LBXAPB    98210 0.969    3.07
 9 LBDAPBSI  98210 0.969    3.07
10 BMXHIP    95277 0.940    5.96
# ℹ 62 more rows

Then we can graph this as:

Code

features_all_percent_compete %>%
  ggplot(aes(x=reorder(feature, PctComp), y =PctComp, fill=PctComp)) +
  geom_bar(stat = "identity") +
  coord_flip() +
  theme(legend.position = "none")

For the remainder of the majority of this discussion we’ll limit ourselves to features that have at least 65% of data:

Code

features_65_num <- Features_Percent_Complete(A_DATA_2.Num, 65) %>%
  filter(feature %in% c(FEATURE_TYPE$numeric_features) )

features_65_num

# A tibble: 18 × 4
   feature              SumNa  PctNa PctComp
   <chr>                <int>  <dbl>   <dbl>
 1 BPXDI3               33989 0.335     66.5
 2 BPXSY3               33988 0.335     66.5
 3 BPXDI2               33382 0.329     67.1
 4 BPXSY2               33382 0.329     67.1
 5 BPXDI1               32740 0.323     67.7
 6 BPXSY1               32740 0.323     67.7
 7 BMXLEG               28483 0.281     71.9
 8 BPXML1               27660 0.273     72.7
 9 BPXPLS               27440 0.271     72.9
10 PEASCTM1             24818 0.245     75.5
11 BMXWAIST             16617 0.164     83.6
12 BMXBMI               13517 0.133     86.7
13 BMXHT                13077 0.129     87.1
14 BMXARMC               9526 0.0940    90.6
15 BMXARML               9505 0.0938    90.6
16 Poverty_Income_Ratio  9196 0.0908    90.9
17 BMXWT                 6134 0.0605    93.9
18 Age                      0 0        100

Note again we can make a function for this graph above:

Code

Feature_Percent_Complete_Graph <- function(data, Percent_Complete = 0 ){
  table <- Features_Percent_Complete(data, Percent_Complete)
  
  plot1 <- table %>%
    mutate(feature = reorder(feature, PctComp)) %>%
    ggplot(aes(x= feature, y =PctComp, fill=PctComp)) +
    geom_bar(stat = "identity") +
    coord_flip() +
    theme(legend.position = "none")
  return(plot1)
}

Let’s time it:

Code

tic <- Sys.time()

Feature_Percent_Complete_Graph(A_DATA_2.Num, 0)

Code

toc <- Sys.time()

FPC.time <- difftime(toc , tic , units = 'secs')

9.4.0.1 Speed-Ups

Amelia is an older package, we can see that our function is

Code

as.numeric(time.Amelia) / as.numeric(FPC.time)

[1] 186.1856

times faster than Amelia::missmap

It also outperforms the mice results by:

Code

as.numeric(time.mice) / as.numeric(FPC.time)

[1] 142.3695

9.4.1 Missing Value Imputation

Note in the below summarise_at we are passing in a number of functions including a function to count the number of missing values n_miss, n, min, max, mean, median, and sd, these summary statistics are computed _at each of the vars we pass in:

Code

summary_table <- A_DATA_2.Num %>%
  filter(!is.na(DIABETES)) %>%
  group_by(Gender, Race, Family_Income) %>%
  summarise( # summarize the data
    across( # apply the following functions to the following columns
      all_of(features_65_num$feature), # select the columns
      list(  # list of functions to apply
        n = ~n(),
        n_miss = ~sum(is.na(.x)),
        min = ~min(.x , na.rm = TRUE),
        max = ~max(.x , na.rm = TRUE),
        mean = ~mean(.x , na.rm = TRUE),
        median = ~median(.x , na.rm = TRUE),
        sd = ~sd(.x , na.rm = TRUE)
        )
      ), # end of across
    .groups='keep' # keep is an option for summary functions
  ) # end of summarise

Warning: There were 40 warnings in `summarise()`.
The first warning was:
ℹ In argument: `across(...)`.
ℹ In group 6: `Gender = "Female"`, `Race = "Black"`, `Family_Income = "$20,000
  and Over"`.
Caused by warning in `min()`:
! no non-missing arguments to min; returning Inf
ℹ Run `dplyr::last_dplyr_warnings()` to see the 39 remaining warnings.

Code

summary_table %>%
  glimpse()

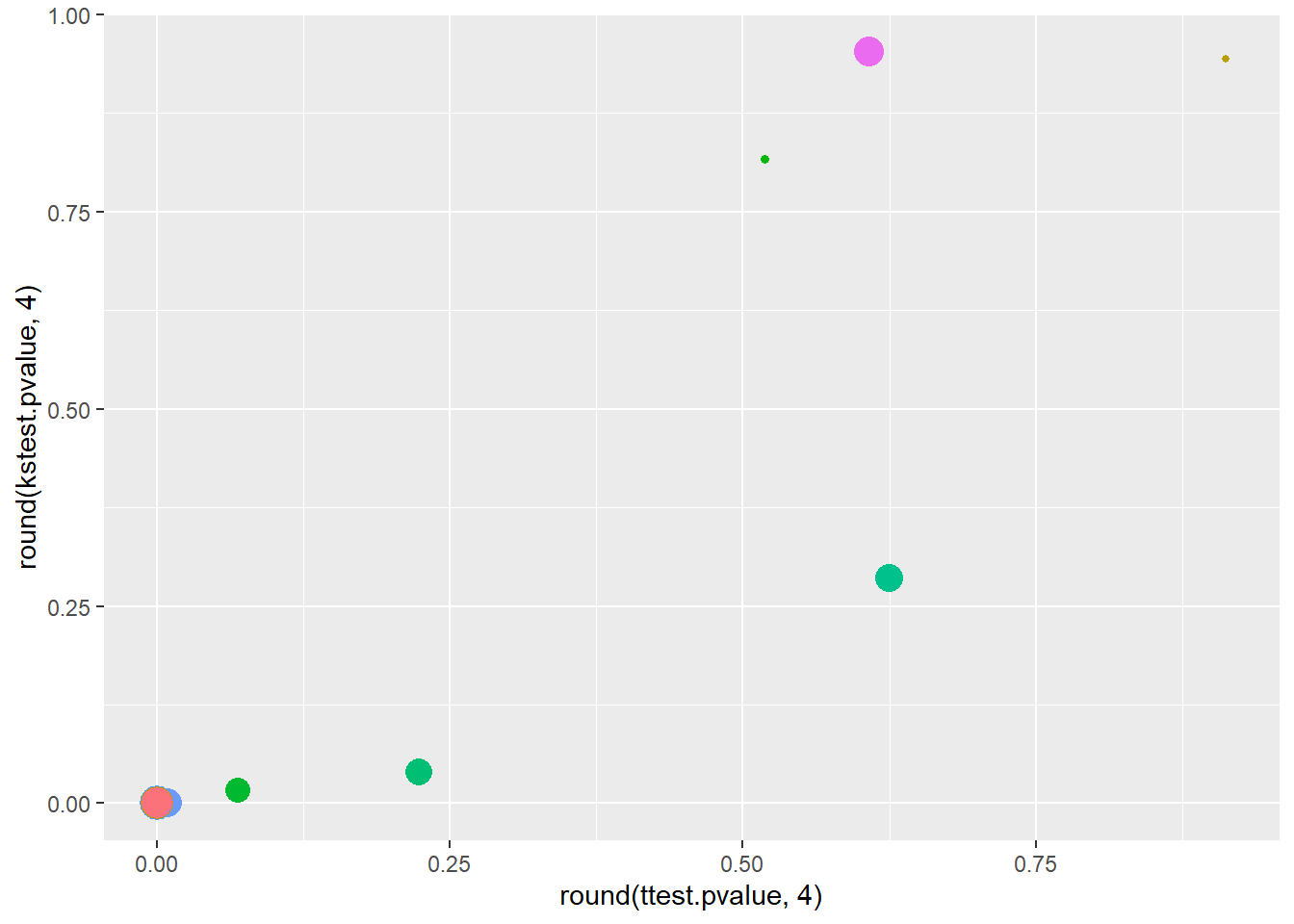
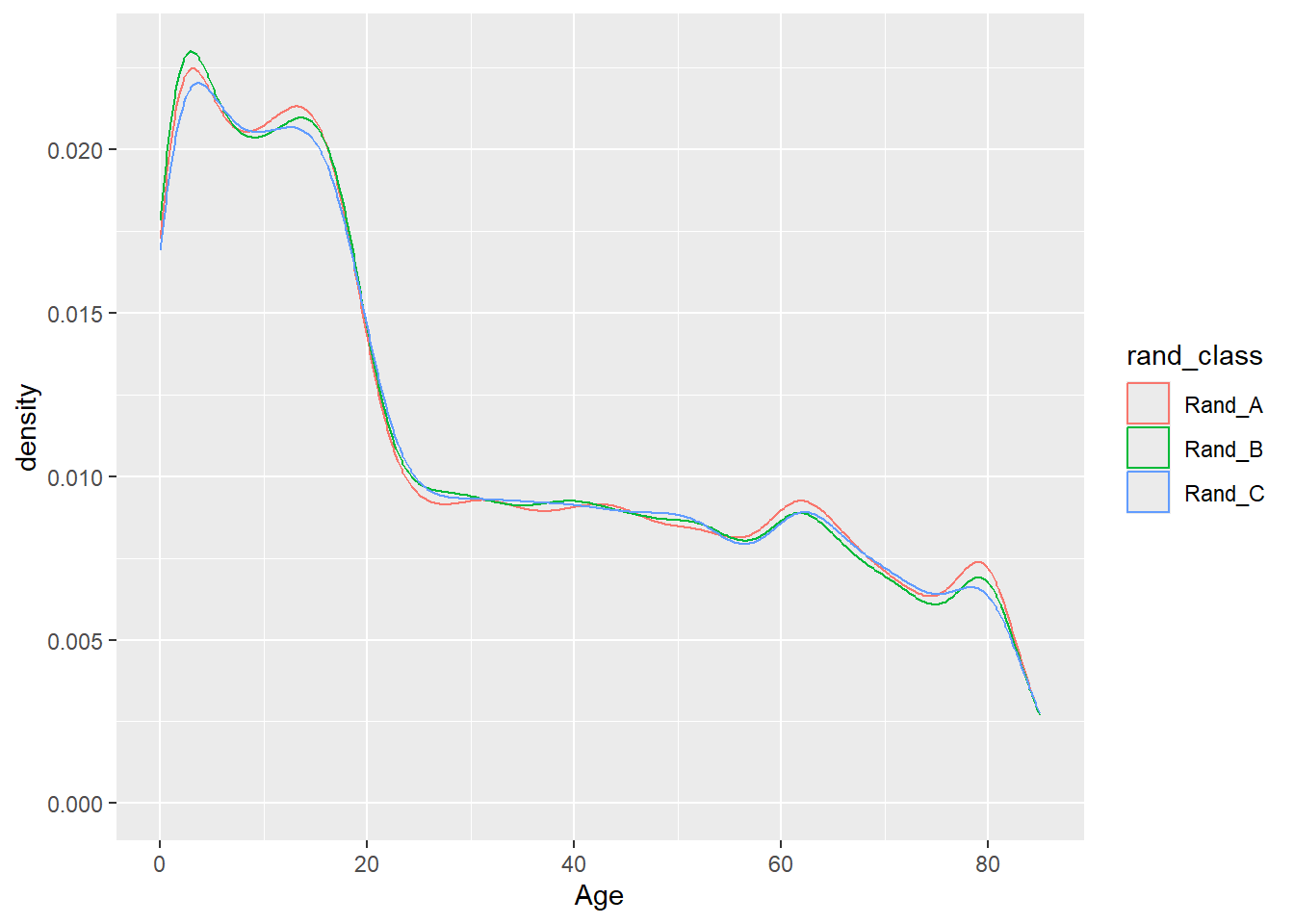
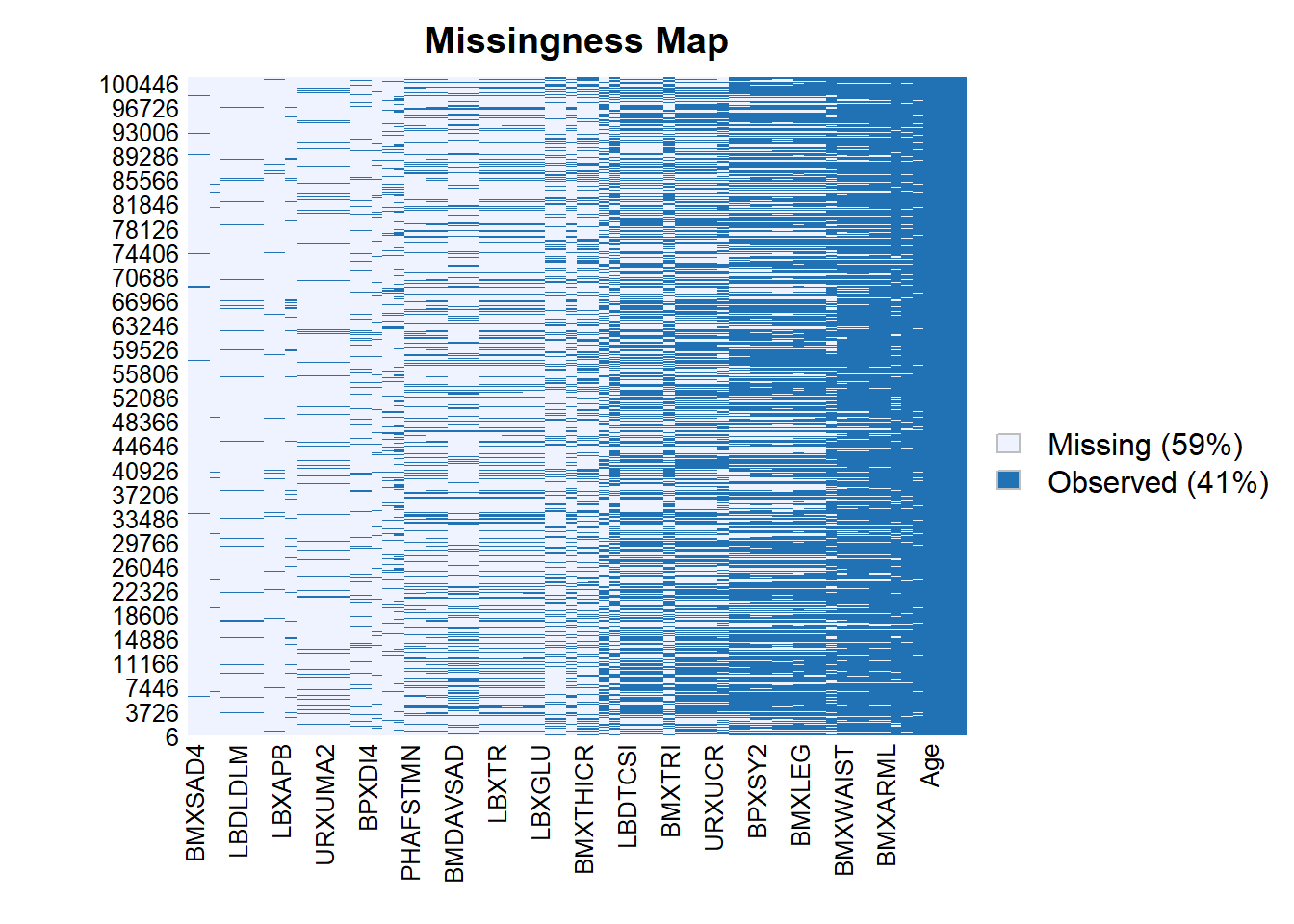
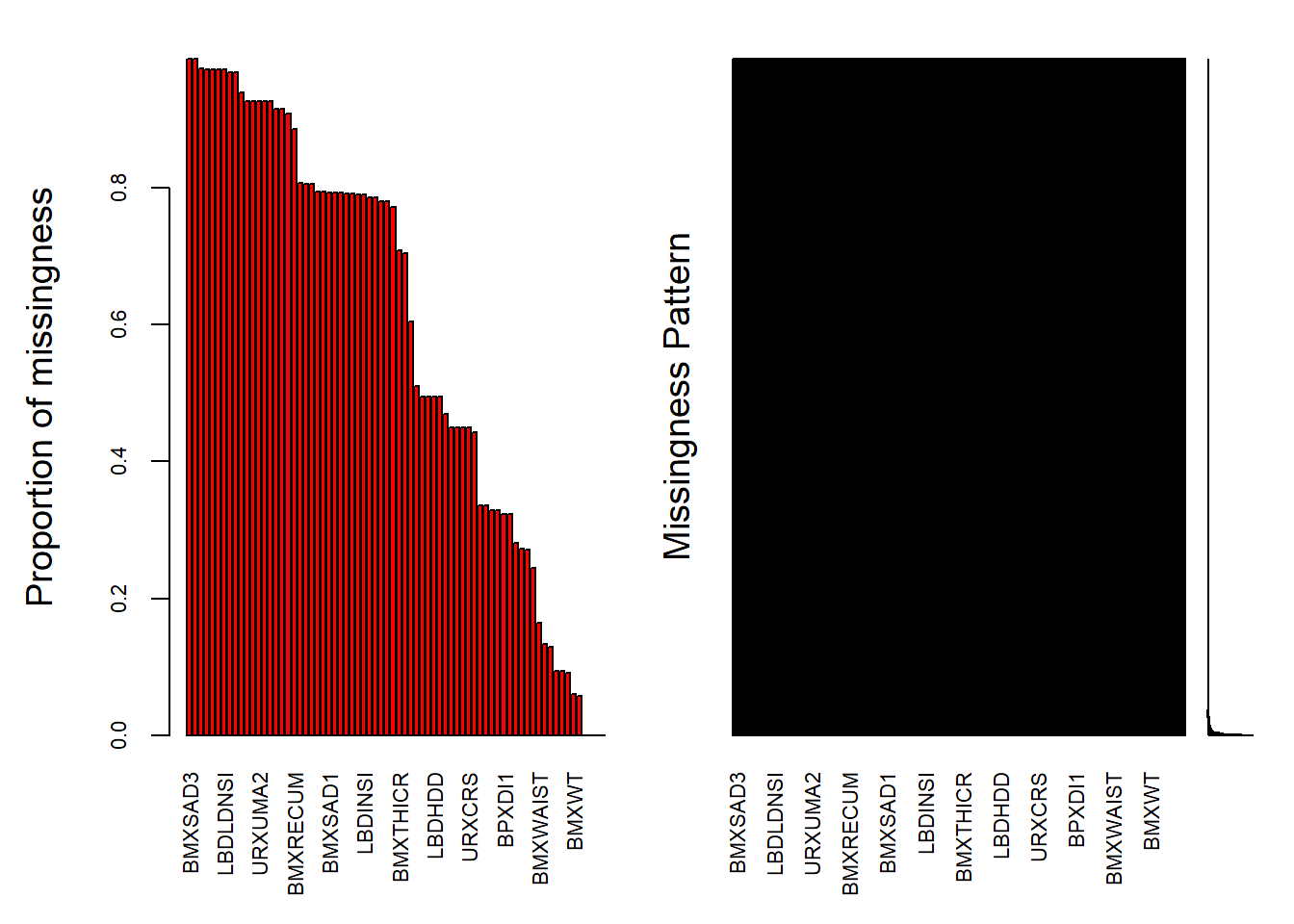
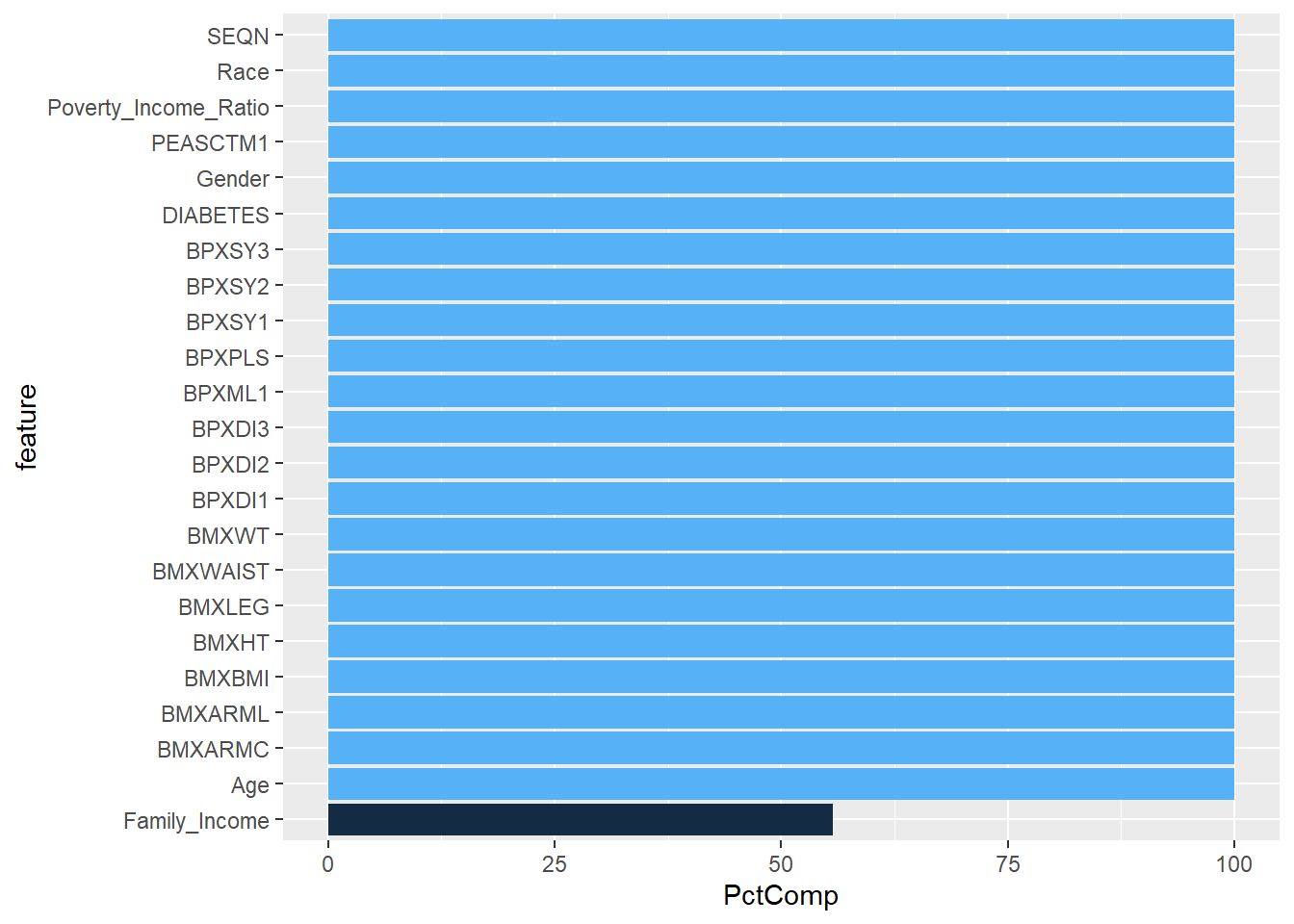
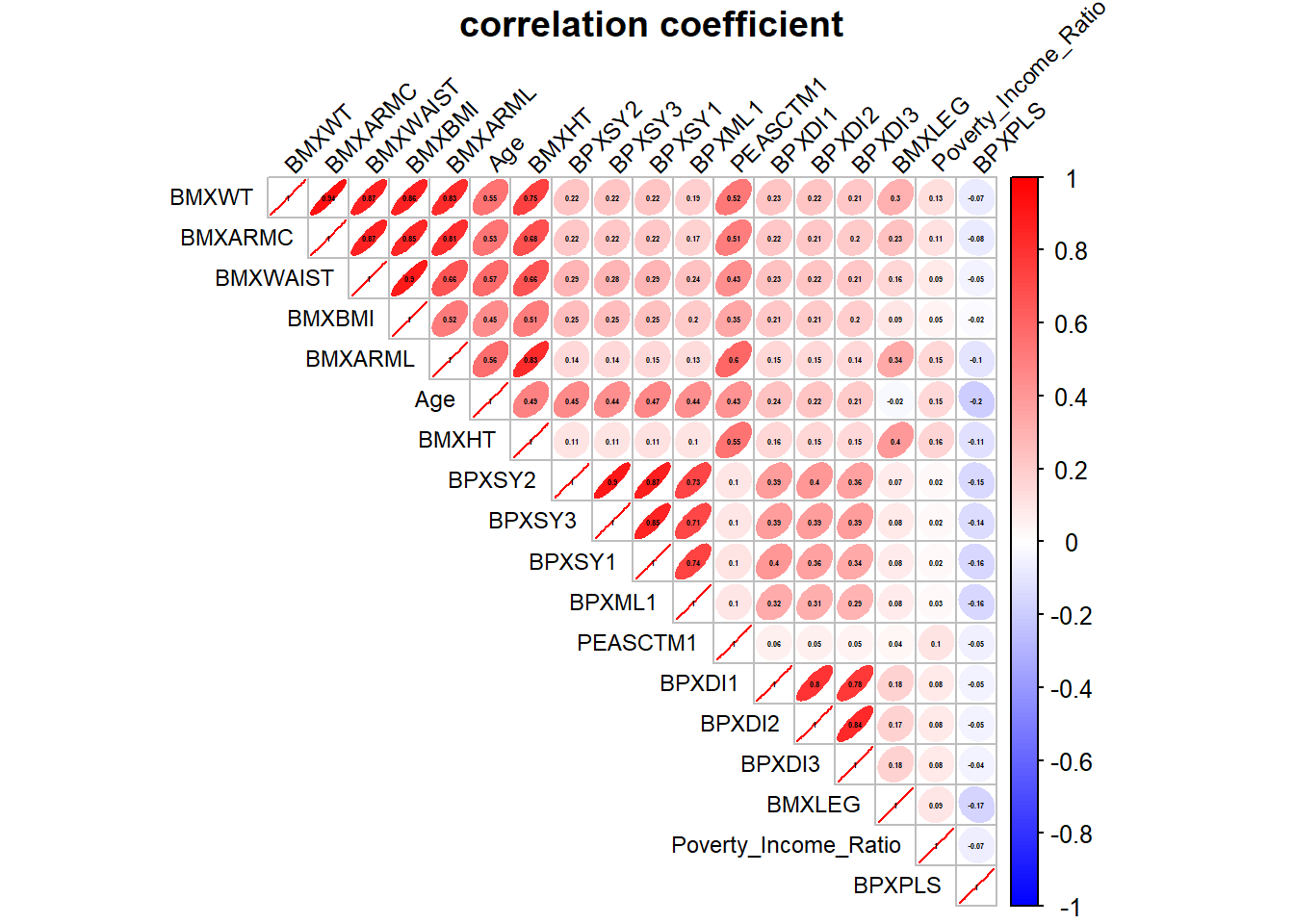
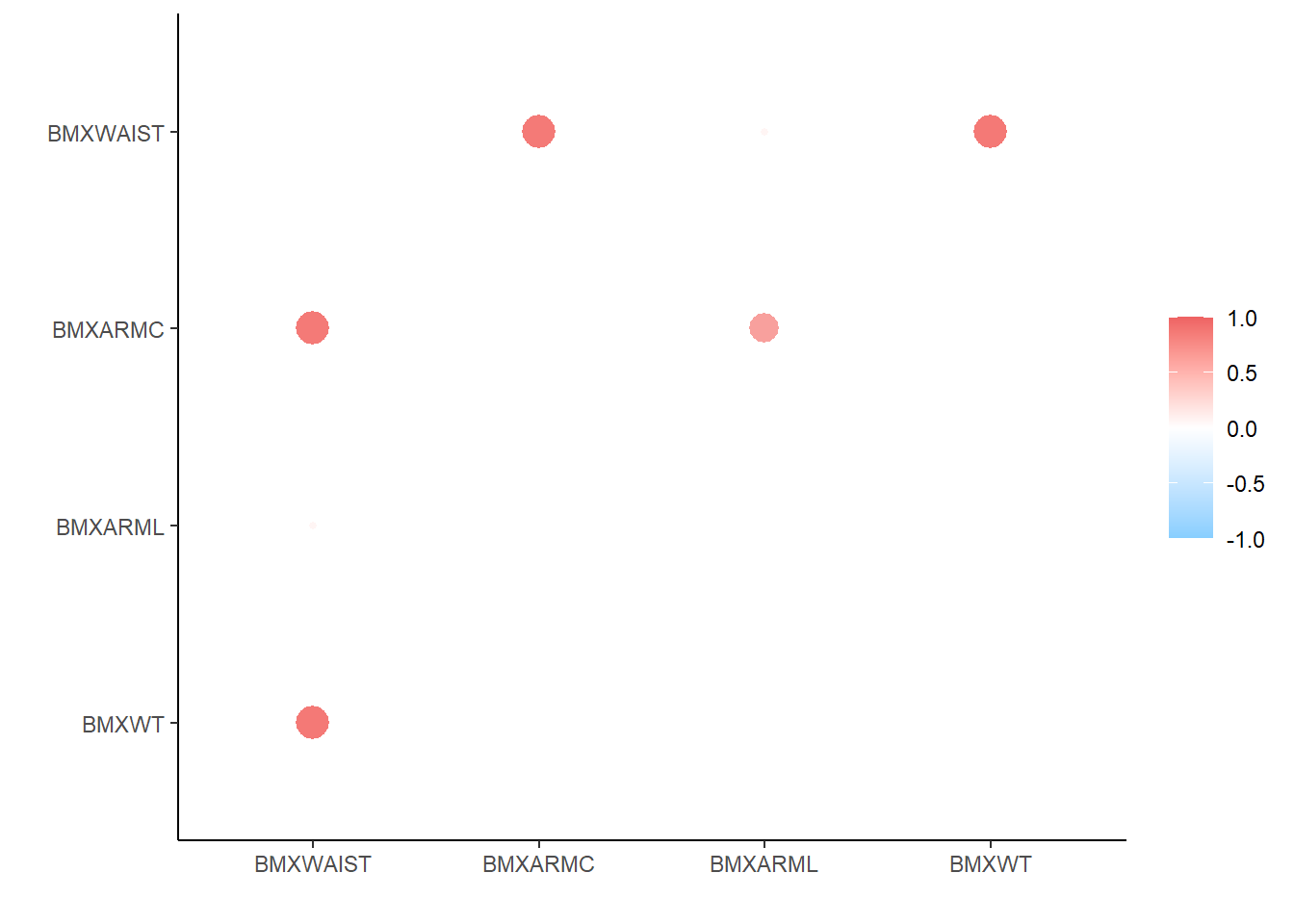
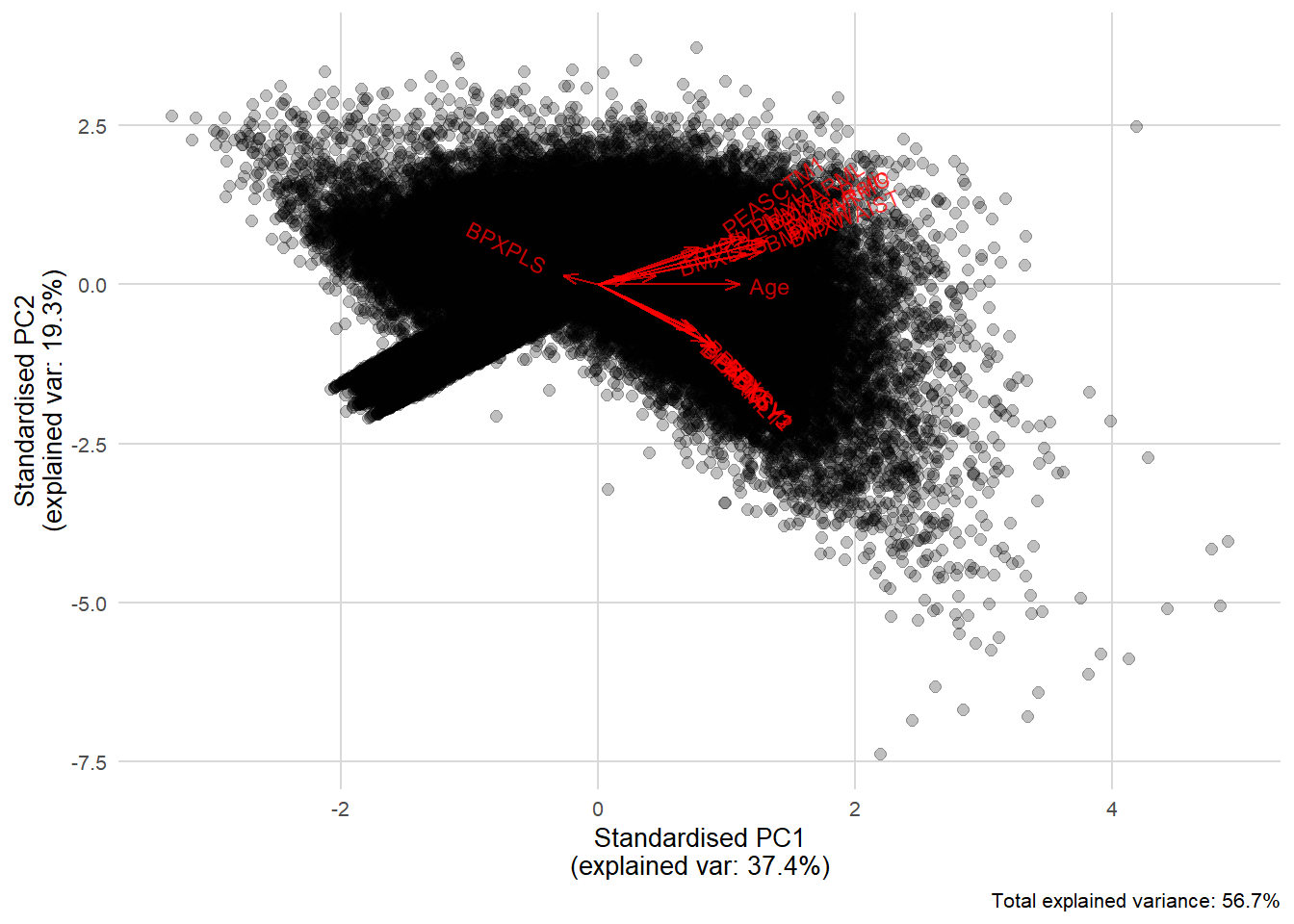
Rows: 150
Columns: 129
Groups: Gender, Race, Family_Income [150]
$ Gender                      <chr> "Female", "Female", "Female", "Female", "F…
$ Race                        <chr> "Black", "Black", "Black", "Black", "Black…
$ Family_Income               <chr> "$ 0 to $ 4,999", "$ 5,000 to $ 9,999", "$…
$ BPXDI3_n                    <int> 364, 459, 522, 541, 456, 171, 544, 827, 57…
$ BPXDI3_n_miss               <int> 110, 142, 155, 117, 136, 36, 134, 206, 138…
$ BPXDI3_min                  <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 26,…
$ BPXDI3_max                  <dbl> 116, 126, 112, 110, 108, 102, 112, 118, 11…
$ BPXDI3_mean                 <dbl> 65.09449, 67.35016, 64.74659, 65.93396, 66…
$ BPXDI3_median               <dbl> 66, 68, 66, 68, 68, 70, 66, 68, 66, 68, 68…
$ BPXDI3_sd                   <dbl> 16.55506, 17.14552, 16.63621, 15.14111, 16…
$ BPXSY3_n                    <int> 364, 459, 522, 541, 456, 171, 544, 827, 57…
$ BPXSY3_n_miss               <int> 110, 142, 155, 117, 136, 36, 134, 206, 138…
$ BPXSY3_min                  <dbl> 84, 82, 74, 82, 86, 80, 82, 80, 78, 82, 86…
$ BPXSY3_max                  <dbl> 224, 212, 218, 210, 196, 222, 212, 232, 20…
$ BPXSY3_mean                 <dbl> 117.7087, 123.9558, 122.2616, 116.7594, 12…
$ BPXSY3_median               <dbl> 114, 118, 116, 112, 116, 122, 114, 116, 11…
$ BPXSY3_sd                   <dbl> 19.76127, 23.39178, 23.76564, 18.70560, 20…
$ BPXDI2_n                    <int> 364, 459, 522, 541, 456, 171, 544, 827, 57…
$ BPXDI2_n_miss               <int> 114, 145, 160, 112, 129, 34, 126, 208, 138…
$ BPXDI2_min                  <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 36,…
$ BPXDI2_max                  <dbl> 126, 124, 110, 114, 110, 104, 108, 122, 11…
$ BPXDI2_mean                 <dbl> 65.25600, 67.51592, 65.16575, 66.54079, 66…
$ BPXDI2_median               <dbl> 66, 66, 66, 68, 68, 68, 66, 66, 66, 66, 66…
$ BPXDI2_sd                   <dbl> 15.90050, 16.45426, 16.46419, 14.67869, 16…
$ BPXSY2_n                    <int> 364, 459, 522, 541, 456, 171, 544, 827, 57…
$ BPXSY2_n_miss               <int> 114, 145, 160, 112, 129, 34, 126, 208, 138…
$ BPXSY2_min                  <dbl> 86, 86, 72, 80, 86, 84, 84, 84, 76, 82, 86…
$ BPXSY2_max                  <dbl> 190, 228, 212, 208, 194, 216, 210, 234, 20…
$ BPXSY2_mean                 <dbl> 117.6400, 125.1401, 123.3702, 117.6364, 12…
$ BPXSY2_median               <dbl> 114, 120, 116, 114, 116, 122, 114, 116, 11…
$ BPXSY2_sd                   <dbl> 19.00957, 23.64783, 23.73587, 18.99184, 21…
$ BPXDI1_n                    <int> 364, 459, 522, 541, 456, 171, 544, 827, 57…
$ BPXDI1_n_miss               <int> 113, 148, 163, 129, 139, 38, 138, 219, 145…
$ BPXDI1_min                  <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 42,…
$ BPXDI1_max                  <dbl> 124, 124, 106, 114, 104, 112, 116, 116, 11…
$ BPXDI1_mean                 <dbl> 66.28685, 68.47588, 65.14206, 66.51942, 66…
$ BPXDI1_median               <dbl> 66, 68, 66, 68, 68, 68, 66, 66, 66, 68, 68…
$ BPXDI1_sd                   <dbl> 14.07457, 15.88685, 15.49407, 13.23757, 15…
$ BPXSY1_n                    <int> 364, 459, 522, 541, 456, 171, 544, 827, 57…
$ BPXSY1_n_miss               <int> 113, 148, 163, 129, 139, 38, 138, 219, 145…
$ BPXSY1_min                  <dbl> 88, 80, 74, 82, 84, 84, 86, 84, 78, 84, 86…
$ BPXSY1_max                  <dbl> 208, 230, 220, 208, 198, 216, 222, 238, 20…
$ BPXSY1_mean                 <dbl> 117.8725, 125.1447, 122.8969, 117.5485, 12…
$ BPXSY1_median               <dbl> 114, 120, 118, 114, 116, 122, 114, 116, 11…
$ BPXSY1_sd                   <dbl> 19.40844, 24.38247, 23.34555, 18.58550, 21…
$ BMXLEG_n                    <int> 364, 459, 522, 541, 456, 171, 544, 827, 57…
$ BMXLEG_n_miss               <int> 116, 139, 165, 111, 134, 35, 126, 199, 129…
$ BMXLEG_min                  <dbl> 27.6, 27.7, 24.9, 27.1, 27.2, 29.8, 28.0, …
$ BMXLEG_max                  <dbl> 47.2, 46.8, 48.2, 48.5, 50.0, 45.0, 46.7, …
$ BMXLEG_mean                 <dbl> 38.63629, 38.14375, 37.86022, 38.96349, 37…
$ BMXLEG_median               <dbl> 38.95, 38.20, 38.00, 39.05, 38.00, 38.30, …
$ BMXLEG_sd                   <dbl> 3.544325, 3.598819, 3.773591, 3.155392, 3.…
$ BPXML1_n                    <int> 364, 459, 522, 541, 456, 171, 544, 827, 57…
$ BPXML1_n_miss               <int> 101, 130, 143, 104, 119, 31, 113, 184, 126…
$ BPXML1_min                  <dbl> 110, 0, 110, 100, 110, 120, 110, 110, 110,…
$ BPXML1_max                  <dbl> 240, 250, 888, 220, 220, 250, 888, 888, 24…
$ BPXML1_mean                 <dbl> 143.3840, 149.3617, 155.3879, 143.5515, 14…
$ BPXML1_median               <dbl> 140, 140, 140, 140, 140, 140, 140, 140, 14…
$ BPXML1_sd                   <dbl> 20.31134, 24.59216, 69.76214, 18.14822, 21…
$ BPXPLS_n                    <int> 364, 459, 522, 541, 456, 171, 544, 827, 57…
$ BPXPLS_n_miss               <int> 101, 131, 142, 104, 119, 31, 113, 183, 126…
$ BPXPLS_min                  <dbl> 50, 46, 46, 44, 46, 50, 46, 46, 50, 48, 36…
$ BPXPLS_max                  <dbl> 120, 116, 130, 120, 112, 110, 140, 118, 12…
$ BPXPLS_mean                 <dbl> 77.87072, 76.92073, 75.43684, 74.52174, 75…
$ BPXPLS_median               <dbl> 78, 76, 74, 74, 74, 74, 76, 76, 74, 74, 74…
$ BPXPLS_sd                   <dbl> 12.51924, 12.55665, 12.28718, 11.47804, 12…
$ PEASCTM1_n                  <int> 364, 459, 522, 541, 456, 171, 544, 827, 57…
$ PEASCTM1_n_miss             <int> 131, 145, 170, 229, 155, 48, 187, 294, 229…
$ PEASCTM1_min                <dbl> 6, 9, 6, 37, 7, 46, 8, 3, 7, 6, 5, 7, 6, 1…
$ PEASCTM1_max                <dbl> 1131, 1536, 1243, 1439, 1274, 1086, 1142, …
$ PEASCTM1_mean               <dbl> 543.7597, 563.0000, 554.6705, 637.6538, 55…
$ PEASCTM1_median             <dbl> 567.0, 576.5, 603.5, 657.5, 590.0, 667.0, …
$ PEASCTM1_sd                 <dbl> 248.5154, 272.9288, 271.9278, 245.9812, 25…
$ BMXWAIST_n                  <int> 364, 459, 522, 541, 456, 171, 544, 827, 57…
$ BMXWAIST_n_miss             <int> 59, 66, 79, 66, 55, 25, 73, 91, 55, 57, 26…
$ BMXWAIST_min                <dbl> 38.7, 43.3, 40.5, 46.2, 42.7, 43.9, 44.2, …
$ BMXWAIST_max                <dbl> 165.5, 171.6, 156.8, 163.5, 158.8, 151.7, …
$ BMXWAIST_mean               <dbl> 83.58656, 89.62290, 88.33115, 89.26379, 84…
$ BMXWAIST_median             <dbl> 80.80, 90.20, 91.60, 89.40, 86.70, 99.60, …
$ BMXWAIST_sd                 <dbl> 25.32800, 26.69575, 25.81373, 21.50595, 24…
$ BMXBMI_n                    <int> 364, 459, 522, 541, 456, 171, 544, 827, 57…
$ BMXBMI_n_miss               <int> 37, 36, 45, 42, 32, 15, 39, 59, 36, 32, 11…
$ BMXBMI_min                  <dbl> 13.40, 12.50, 13.41, 13.40, 12.70, 13.30, …
$ BMXBMI_max                  <dbl> 57.80, 82.10, 77.50, 68.70, 84.40, 64.70, …
$ BMXBMI_mean                 <dbl> 26.12003, 27.81638, 27.77199, 27.98603, 26…
$ BMXBMI_median               <dbl> 23.700, 26.660, 27.230, 26.900, 25.500, 30…
$ BMXBMI_sd                   <dbl> 9.509575, 10.418529, 9.889805, 8.842373, 9…
$ BMXHT_n                     <int> 364, 459, 522, 541, 456, 171, 544, 827, 57…
$ BMXHT_n_miss                <int> 36, 36, 44, 42, 32, 14, 39, 59, 34, 32, 11…
$ BMXHT_min                   <dbl> 78.5, 81.6, 82.8, 86.0, 82.5, 92.3, 86.9, …
$ BMXHT_max                   <dbl> 184.8, 186.4, 180.9, 187.8, 184.1, 177.4, …
$ BMXHT_mean                  <dbl> 148.9064, 150.9000, 150.5358, 156.7822, 15…
$ BMXHT_median                <dbl> 158.45, 159.00, 158.35, 161.40, 158.50, 16…
$ BMXHT_sd                    <dbl> 23.88131, 22.45114, 21.96616, 16.70671, 22…
$ BMXARMC_n                   <int> 364, 459, 522, 541, 456, 171, 544, 827, 57…
$ BMXARMC_n_miss              <int> 41, 40, 58, 44, 41, 20, 50, 65, 39, 42, 20…
$ BMXARMC_min                 <dbl> 13.8, 13.8, 13.9, 14.6, 13.7, 14.0, 13.1, …
$ BMXARMC_max                 <dbl> 54.0, 57.3, 51.7, 58.1, 48.5, 51.5, 58.3, …
$ BMXARMC_mean                <dbl> 28.14458, 29.31217, 29.28405, 30.31288, 28…
$ BMXARMC_median              <dbl> 28.00, 29.80, 30.10, 30.70, 29.30, 32.50, …
$ BMXARMC_sd                  <dbl> 8.507530, 9.030110, 8.539857, 7.509531, 8.…
$ BMXARML_n                   <int> 364, 459, 522, 541, 456, 171, 544, 827, 57…
$ BMXARML_n_miss              <int> 43, 42, 57, 45, 40, 22, 52, 66, 39, 42, 21…
$ BMXARML_min                 <dbl> 13.9, 15.0, 14.4, 16.0, 14.0, 15.6, 16.0, …
$ BMXARML_max                 <dbl> 42.0, 43.9, 43.2, 43.0, 43.9, 41.9, 43.0, …
$ BMXARML_mean                <dbl> 32.38505, 32.86547, 33.19505, 34.53145, 32…
$ BMXARML_median              <dbl> 34.60, 35.40, 35.70, 36.00, 35.15, 36.00, …
$ BMXARML_sd                  <dbl> 6.895394, 6.810559, 6.819470, 5.132052, 6.…
$ Poverty_Income_Ratio_n      <int> 364, 459, 522, 541, 456, 171, 544, 827, 57…
$ Poverty_Income_Ratio_n_miss <int> 0, 0, 0, 0, 0, 171, 0, 0, 0, 0, 0, 0, 0, 1…
$ Poverty_Income_Ratio_min    <dbl> 0.00, 0.12, 0.27, 2.25, 0.30, Inf, 0.48, 0…
$ Poverty_Income_Ratio_max    <dbl> 0.43, 0.95, 1.35, 5.00, 1.85, -Inf, 2.31, …
$ Poverty_Income_Ratio_mean   <dbl> 0.10730769, 0.46331155, 0.70402299, 4.6876…
$ Poverty_Income_Ratio_median <dbl> 0.085, 0.410, 0.680, 5.000, 0.860, NA, 1.0…
$ Poverty_Income_Ratio_sd     <dbl> 0.09773131, 0.20340318, 0.26553590, 0.5764…
$ BMXWT_n                     <int> 364, 459, 522, 541, 456, 171, 544, 827, 57…
$ BMXWT_n_miss                <int> 24, 17, 30, 27, 22, 9, 23, 36, 21, 19, 6, …
$ BMXWT_min                   <dbl> 7.7, 8.9, 8.5, 10.0, 8.9, 10.0, 8.9, 8.2, …
$ BMXWT_max                   <dbl> 157.5, 187.7, 191.6, 193.7, 219.6, 173.4, …
$ BMXWT_mean                  <dbl> 60.84735, 65.91312, 66.12337, 70.02490, 63…
$ BMXWT_median                <dbl> 59.65, 67.10, 70.05, 70.55, 64.95, 76.75, …
$ BMXWT_sd                    <dbl> 33.33993, 35.45615, 33.77805, 29.73478, 33…
$ Age_n                       <int> 364, 459, 522, 541, 456, 171, 544, 827, 57…
$ Age_n_miss                  <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ Age_min                     <dbl> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, …
$ Age_max                     <dbl> 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80…
$ Age_mean                    <dbl> 24.66484, 33.91285, 35.53831, 33.82994, 31…
$ Age_median                  <dbl> 19.0, 28.0, 31.0, 35.0, 24.0, 42.0, 26.0, …
$ Age_sd                      <dbl> 20.24840, 25.68241, 26.35764, 22.24478, 25…

We can actually restructure this table if we use some dplyr:

Code

summary_table %>%
  pivot_longer(cols = contains(features_65_num$feature))

# A tibble: 18,900 × 5
# Groups:   Gender, Race, Family_Income [150]
   Gender Race  Family_Income  name          value
   <chr>  <chr> <chr>          <chr>         <dbl>
 1 Female Black $ 0 to $ 4,999 BPXDI3_n      364  
 2 Female Black $ 0 to $ 4,999 BPXDI3_n_miss 110  
 3 Female Black $ 0 to $ 4,999 BPXDI3_min      0  
 4 Female Black $ 0 to $ 4,999 BPXDI3_max    116  
 5 Female Black $ 0 to $ 4,999 BPXDI3_mean    65.1
 6 Female Black $ 0 to $ 4,999 BPXDI3_median  66  
 7 Female Black $ 0 to $ 4,999 BPXDI3_sd      16.6
 8 Female Black $ 0 to $ 4,999 BPXSY3_n      364  
 9 Female Black $ 0 to $ 4,999 BPXSY3_n_miss 110  
10 Female Black $ 0 to $ 4,999 BPXSY3_min     84  
# ℹ 18,890 more rows

We can also just focus on the counts of missing values:

Code

summary_table %>%
  pivot_longer(cols = contains(features_65_num$feature)) %>%
  filter(str_detect(name, "n_miss")) %>%
  arrange(-value)

# A tibble: 2,700 × 5
# Groups:   Gender, Race, Family_Income [150]
   Gender Race  Family_Income name          value
   <chr>  <chr> <chr>         <chr>         <dbl>
 1 Female White <NA>          BPXDI3_n_miss  2701
 2 Female White <NA>          BPXSY3_n_miss  2700
 3 Female White <NA>          BPXDI2_n_miss  2619
 4 Female White <NA>          BPXSY2_n_miss  2619
 5 Male   White <NA>          BPXDI3_n_miss  2516
 6 Male   White <NA>          BPXSY3_n_miss  2516
 7 Male   White <NA>          BPXDI2_n_miss  2488
 8 Male   White <NA>          BPXSY2_n_miss  2488
 9 Female White <NA>          BPXDI1_n_miss  2366
10 Female White <NA>          BPXSY1_n_miss  2366
# ℹ 2,690 more rows

We can impute missing values with the mean for the column, perhaps by Gender, Race, Family_Income

Code

A_DATA_2.Num.impute <- A_DATA_2.Num %>%
  filter(!is.na(DIABETES)) %>%
  mutate(
    across(
      c("Gender", "Race"), 
      \(x){if_else(is.na(x), "Missing", x)}
      )) %>%
  group_by(Gender, Race) %>%
  mutate(
    across(
      all_of(features_65_num$feature),  
      \(x){if_else(is.na(x), mean(x, na.rm = TRUE), x)}
      )
    ) %>%
  ungroup() %>%
  select(SEQN, DIABETES, Gender, Race, Family_Income, all_of(features_65_num$feature))

We can recompute our summary table - and if we were so inclined see if any of these values changed significantly:

Code

A_DATA_2.Num.impute %>%
  group_by(Gender, Race, Family_Income) %>%
  summarise(
    across(
      all_of(features_65_num$feature), # select the numeric features
      list( # list of functions to apply
        n = ~n(),
        n_miss = ~sum(is.na(.)),
        min = ~min(. , na.rm = TRUE),
        max = ~max(. , na.rm = TRUE),
        mean = ~mean(. , na.rm = TRUE),
        median = ~median(. , na.rm = TRUE),
        sd = ~sd(. , na.rm = TRUE)
        ) # end list
      ), # end across
    .groups='keep' # keep the groups is a summarise option
    ) %>% # end summarise
  ungroup() %>% # ungroup the data
  pivot_longer(contains(features_65_num$feature)) %>% # pivot the data
  filter(str_detect(name,"n_miss")) %>%
  arrange(-value)

# A tibble: 2,700 × 5
   Gender Race  Family_Income  name            value
   <chr>  <chr> <chr>          <chr>           <dbl>
 1 Female Black $ 0 to $ 4,999 BPXDI3_n_miss       0
 2 Female Black $ 0 to $ 4,999 BPXSY3_n_miss       0
 3 Female Black $ 0 to $ 4,999 BPXDI2_n_miss       0
 4 Female Black $ 0 to $ 4,999 BPXSY2_n_miss       0
 5 Female Black $ 0 to $ 4,999 BPXDI1_n_miss       0
 6 Female Black $ 0 to $ 4,999 BPXSY1_n_miss       0
 7 Female Black $ 0 to $ 4,999 BMXLEG_n_miss       0
 8 Female Black $ 0 to $ 4,999 BPXML1_n_miss       0
 9 Female Black $ 0 to $ 4,999 BPXPLS_n_miss       0
10 Female Black $ 0 to $ 4,999 PEASCTM1_n_miss     0
# ℹ 2,690 more rows

But for now let’s just look at the number of missing values:

Code

Feature_Percent_Complete_Graph(A_DATA_2.Num.impute,0)

9.5 Correlated Features

Often we will want to search for highly correlated features in order to reduce the number of them in a model.

In the extreme case, consider some variables that are perfectly correlated, i.e. linearly dependent.

Let’s say you’re using logistic regression to predict the probability of having Diabetes, where one of the predictor variables will be Age, but for some reason you read in two input variables \(x_1\) = Age in months and \(x_2\) = Age in years. Clearly, \(x_1\) and \(x_2\) are linearly dependent as \[x_1 \cdot 12 = x_2 \].

In your model, you will estimate coefficients \(\beta_i\) such that

\[\log \left( \frac{P(DIABETES == 1)}{P(DIABETES == 0)} \right)=\beta_0+\beta_1x_1+\beta_2x_2+(\cdots)\]

Due to the linear dependence, we can rewrite this:

\[\log \left( \frac{P(DIABETES == 1)}{P(DIABETES == 0)} \right)=\beta_0 + \beta_1x_1 + \beta_2\cdot ( x_1 \cdot 12) + (\cdots)\]

\[\log \left( \frac{P(DIABETES == 1)}{P(DIABETES == 0)} \right)=\beta_0 + x_1 ( \beta_1 + 12 \cdot \beta_2 ) + (\cdots)\]

SUPPOSE (for some reason) that the Age in years has no influence on Diabetic status.

Then you would expect your model to find \[\beta_1 = \beta_2=0\].

However, due to linear dependence, the model cannot distinguish between \(\beta_1=12\), \(\beta_2 = -1\) or any other combination where \(\beta_1 + 12 \cdot \beta_2 = 0\)

Thus on the one hand, your model itself might become numerically unstable. On the other hand, you can no longer interpret the results correctly.

The same is true when variables are no longer linearly dependent but highly correlated.

Code

library(corrplot)

corrplot 0.92 loaded

Code

tmwr_cols <- colorRampPalette(c("blue","white", "red"))

combined_data_cor_prep <- A_DATA_2.Num.impute %>%
  select(all_of(features_65_num$feature))  

cor_res <- Hmisc::rcorr(as.matrix(combined_data_cor_prep))


combined_data_cor_prep %>%
  #rename_all(~paste0("c", seq_along(.))) %>%
  na.omit() %>%
  cor() %>% 
  corrplot::corrplot(
    col = tmwr_cols(200), 
    tl.col = "black", 
    method = "ellipse",
    order ='FPC',
    type = "upper",
    title = "Correlated Features Plot \n correlation coefficient",
    addCoef.col = "black",
    number.cex = 0.25,
    tl.cex = 0.75,           # Size of the feature labels
    tl.srt = 45)

Code

library('corrr')
cor.corr_data <- correlate(A_DATA_2.Num.impute %>% select(all_of(features_65_num$feature)))

Correlation computed with
• Method: 'pearson'
• Missing treated using: 'pairwise.complete.obs'

Code

cor.corr_data %>%
  glimpse()

Rows: 18
Columns: 19
$ term                 <chr> "BPXDI3", "BPXSY3", "BPXDI2", "BPXSY2", "BPXDI1",…
$ BPXDI3               <dbl> NA, 0.38920867, 0.83967525, 0.36443328, 0.7753937…
$ BPXSY3               <dbl> 0.38920867, NA, 0.38726807, 0.90335402, 0.3855849…
$ BPXDI2               <dbl> 0.83967525, 0.38726807, NA, 0.40498199, 0.7965398…
$ BPXSY2               <dbl> 0.36443328, 0.90335402, 0.40498199, NA, 0.3885915…
$ BPXDI1               <dbl> 0.77539372, 0.38558496, 0.79653986, 0.38859151, N…
$ BPXSY1               <dbl> 0.33796063, 0.85488694, 0.36272962, 0.87340339, 0…
$ BMXLEG               <dbl> 0.17755182, 0.08128816, 0.17371484, 0.07458496, 0…
$ BPXML1               <dbl> 0.29189725, 0.71441600, 0.31253493, 0.72838772, 0…
$ BPXPLS               <dbl> -0.04218378, -0.13904054, -0.04813751, -0.1459656…
$ PEASCTM1             <dbl> 0.04786246, 0.09740853, 0.05094561, 0.09772117, 0…
$ BMXWAIST             <dbl> 0.21484511, 0.28490823, 0.22377722, 0.28689614, 0…
$ BMXBMI               <dbl> 0.19847274, 0.25144750, 0.20672813, 0.25229207, 0…
$ BMXHT                <dbl> 0.1497063, 0.1099074, 0.1519246, 0.1080122, 0.157…
$ BMXARMC              <dbl> 0.20485012, 0.21875540, 0.21110377, 0.21854444, 0…
$ BMXARML              <dbl> 0.1432836, 0.1448157, 0.1464210, 0.1440410, 0.152…
$ Poverty_Income_Ratio <dbl> 0.08229314, 0.02244386, 0.08448418, 0.02402425, 0…
$ BMXWT                <dbl> 0.21497276, 0.22357424, 0.22145776, 0.22239343, 0…
$ Age                  <dbl> 0.20551574, 0.43888769, 0.22400775, 0.45189382, 0…

Let’s find all the rows where Age has a correlation of .5 or more with another variable.

Code

cor.corr_data %>%
   filter(Age > .5)

# A tibble: 4 × 19
  term  BPXDI3 BPXSY3 BPXDI2 BPXSY2 BPXDI1 BPXSY1 BMXLEG BPXML1  BPXPLS PEASCTM1
  <chr>  <dbl>  <dbl>  <dbl>  <dbl>  <dbl>  <dbl>  <dbl>  <dbl>   <dbl>    <dbl>
1 BMXW…  0.215  0.285  0.224  0.287  0.233  0.287  0.157  0.238 -0.0462    0.432
2 BMXA…  0.205  0.219  0.211  0.219  0.219  0.217  0.231  0.173 -0.0769    0.510
3 BMXA…  0.143  0.145  0.146  0.144  0.153  0.148  0.339  0.131 -0.104     0.599
4 BMXWT  0.215  0.224  0.221  0.222  0.229  0.220  0.301  0.187 -0.0701    0.521
# ℹ 8 more variables: BMXWAIST <dbl>, BMXBMI <dbl>, BMXHT <dbl>, BMXARMC <dbl>,
#   BMXARML <dbl>, Poverty_Income_Ratio <dbl>, BMXWT <dbl>, Age <dbl>

Let’s find all the rows where any feature has a correlation of .7 or more with another variable:

Code

cor.corr_data %>%
   filter_at(vars(all_of(features_65_num$feature)), any_vars( . > .7 ))

# A tibble: 13 × 19
   term     BPXDI3 BPXSY3 BPXDI2 BPXSY2 BPXDI1 BPXSY1 BMXLEG BPXML1  BPXPLS
   <chr>     <dbl>  <dbl>  <dbl>  <dbl>  <dbl>  <dbl>  <dbl>  <dbl>   <dbl>
 1 BPXDI3   NA      0.389  0.840  0.364  0.775  0.338 0.178   0.292 -0.0422
 2 BPXSY3    0.389 NA      0.387  0.903  0.386  0.855 0.0813  0.714 -0.139 
 3 BPXDI2    0.840  0.387 NA      0.405  0.797  0.363 0.174   0.313 -0.0481
 4 BPXSY2    0.364  0.903  0.405 NA      0.389  0.873 0.0746  0.728 -0.146 
 5 BPXDI1    0.775  0.386  0.797  0.389 NA      0.404 0.178   0.320 -0.0498
 6 BPXSY1    0.338  0.855  0.363  0.873  0.404 NA     0.0773  0.739 -0.156 
 7 BPXML1    0.292  0.714  0.313  0.728  0.320  0.739 0.0799 NA     -0.157 
 8 BMXWAIST  0.215  0.285  0.224  0.287  0.233  0.287 0.157   0.238 -0.0462
 9 BMXBMI    0.198  0.251  0.207  0.252  0.213  0.247 0.0948  0.202 -0.0185
10 BMXHT     0.150  0.110  0.152  0.108  0.157  0.112 0.397   0.105 -0.114 
11 BMXARMC   0.205  0.219  0.211  0.219  0.219  0.217 0.231   0.173 -0.0769
12 BMXARML   0.143  0.145  0.146  0.144  0.153  0.148 0.339   0.131 -0.104 
13 BMXWT     0.215  0.224  0.221  0.222  0.229  0.220 0.301   0.187 -0.0701
# ℹ 9 more variables: PEASCTM1 <dbl>, BMXWAIST <dbl>, BMXBMI <dbl>,
#   BMXHT <dbl>, BMXARMC <dbl>, BMXARML <dbl>, Poverty_Income_Ratio <dbl>,
#   BMXWT <dbl>, Age <dbl>

Above we used an _at version of a dplyr function, in this case it will apply the function any_vars( . > .7 ) to the columns corr_features.

Code

cor.corr_data %>% 
  focus(BMXWT, BMXARMC, BMXARML, BMXWAIST)

# A tibble: 14 × 5
   term                   BMXWT BMXARMC BMXARML BMXWAIST
   <chr>                  <dbl>   <dbl>   <dbl>    <dbl>
 1 BPXDI3                0.215   0.205    0.143   0.215 
 2 BPXSY3                0.224   0.219    0.145   0.285 
 3 BPXDI2                0.221   0.211    0.146   0.224 
 4 BPXSY2                0.222   0.219    0.144   0.287 
 5 BPXDI1                0.229   0.219    0.153   0.233 
 6 BPXSY1                0.220   0.217    0.148   0.287 
 7 BMXLEG                0.301   0.231    0.339   0.157 
 8 BPXML1                0.187   0.173    0.131   0.238 
 9 BPXPLS               -0.0701 -0.0769  -0.104  -0.0462
10 PEASCTM1              0.521   0.510    0.599   0.432 
11 BMXBMI                0.861   0.846    0.516   0.895 
12 BMXHT                 0.747   0.681    0.830   0.665 
13 Poverty_Income_Ratio  0.128   0.111    0.151   0.0895
14 Age                   0.550   0.533    0.563   0.575

Code

cor.corr_data %>%
  focus(BMXWT, BMXARMC, BMXARML, BMXWAIST, mirror = TRUE) %>%  # Focus only on these
  shave() %>% # Remove the upper triangle
  fashion()   # Print in nice format

      term BMXWT BMXARMC BMXARML BMXWAIST
1 BMXWAIST   .87                         
2  BMXARMC   .94                         
3  BMXARML   .83     .81                 
4    BMXWT           .94     .83      .87

Code

cor.corr_data %>%
  focus(BMXWT, BMXARMC, BMXARML, BMXWAIST, mirror = TRUE) %>%
  shave(upper = FALSE) %>% 
  rplot(colours = c("skyblue1", "white",  "indianred2"))

The findCorrelation function in the caret library is useful to find correlated features as well:

Code

correlated_features <- caret::findCorrelation( cor(A_DATA_2.Num.impute %>% select(all_of(features_65_num$feature)) ),
                        cutoff = .8,
                        names = TRUE )

correlated_features

[1] "BMXWT"    "BMXARMC"  "BMXWAIST" "BMXARML"  "BPXSY2"   "BPXSY3"   "BPXDI2"

9.6 Principal Component Analysis

Principal Component Analysis describes an orthogonal (preserves inner product) linear transformation of the data; where the data are mapped into a new coordinate system for which the first dimension (the first principal component) contains the greatest variance of the data; the second dimension contains the second greatest variance; and so on.

We will showcase how Principal Component Analysis (PCA) can yield the Principal Components (PCs) can be utilized as effectively as features in a predictive model.

First will split the data:

Code

set.seed(4321)

A_DATA_2.Num.impute <- A_DATA_2.Num.impute %>%
  mutate(DIABETES_factor = as.factor(DIABETES))


PCA_train.sample <- sample(A_DATA_2.Num.impute$SEQN,
                    nrow(A_DATA_2.Num.impute)*.65,
                    replace = FALSE)

PCA.train <- A_DATA_2.Num.impute %>%
  filter(SEQN %in% PCA_train.sample) 

PCA.test <- A_DATA_2.Num.impute %>%
  filter(!(SEQN %in% PCA_train.sample))

9.6.1 Fit PCA Model

Below, we set center and scale to TRUE so R will center (subtract the mean) and scale (divide by the standard deviation) by each numeric column (i.e., z-score, normalize. or standardize the data). Now we can fit a PCA model on the training data:

Code

A_DATA_2.pca.model <- prcomp(PCA.train %>% select(all_of(features_65_num$feature)), 
                              center=TRUE,
                              scale=TRUE)

A_DATA_2.pca.sum <- summary(A_DATA_2.pca.model)
A_DATA_2.pca.sum

Importance of components:
                          PC1    PC2    PC3     PC4     PC5     PC6     PC7
Standard deviation     2.5949 1.8632 1.3535 1.11351 0.99700 0.92733 0.90471
Proportion of Variance 0.3741 0.1929 0.1018 0.06888 0.05522 0.04777 0.04547
Cumulative Proportion  0.3741 0.5669 0.6687 0.73760 0.79282 0.84060 0.88607
                           PC8     PC9    PC10    PC11    PC12    PC13    PC14
Standard deviation     0.67546 0.54761 0.50835 0.49355 0.48052 0.40548 0.36967
Proportion of Variance 0.02535 0.01666 0.01436 0.01353 0.01283 0.00913 0.00759
Cumulative Proportion  0.91142 0.92808 0.94243 0.95597 0.96880 0.97793 0.98552
                          PC15    PC16    PC17    PC18
Standard deviation     0.30145 0.29972 0.22785 0.16732
Proportion of Variance 0.00505 0.00499 0.00288 0.00156
Cumulative Proportion  0.99057 0.99556 0.99844 1.00000

You can see there are 18 principal components, with each explaining a proportion of the variability in the data. For example, PC1 explains 37.407% of the total variance; the first 5 principal components account for over 79.282% of the variance; the first 10 principal components account for over 94.243% of the variance.

9.6.2 Plot Principal Components

The biplot is used to visualize principal components. This plots the first and second principal components. The closer the variable is the the center, the less contribution that variable has to either principal component. The configuration of arrows reflects the relations of the variables. The cosine of the angle (the dot product) between the arrows reflects the correlation between the variables they represent, and the principal component.

Code

AMR::ggplot_pca(A_DATA_2.pca.model, arrows_colour = 'red') # note here that the assumption is to plot PC1 V PC2

This is the first versus the third principal component, again notice the magnitude and direction of the vector with relation to the first principal component:

Code

AMR::ggplot_pca(A_DATA_2.pca.model,
                choices = c(1,3), # here we specify PC1 V PC3 
                arrows_colour = 'red')

And now here’s a look at the second versus the third, we see everything is concentrated near the origin (Remark when we zoomed in with coord_cartesian some points were excluded from the Figure below)

Code

AMR::ggplot_pca(A_DATA_2.pca.model,
                choices = c(2,3),
                arrows_colour = 'red',
                arrows_size = 1,
                arrows_textsize = 4) +
  coord_cartesian(xlim = c(-5,5), ylim=c(-5,5))

9.6.3 Scree Plot

We aim to find the components with the maximum variance so we can retain as much information about the original dataset as possible.

To determine the number of principal components to retain in our analysis we need to compute the proportion of variance explained.

We can plot the cumulative proportion of variance explained in a scree plot to determine the number of principal components to retain:

Code

var_exp <- A_DATA_2.pca.model$sdev^2

# Proportion of variance explained
pct_var_exp <- var_exp/sum(var_exp)

Prop_Var_Explained_df <- as_tibble(cbind(var_exp, pct_var_exp))

Prop_Var_Explained_df$PC <- 1:nrow(Prop_Var_Explained_df)


Prop_Var_Explained_df <- Prop_Var_Explained_df %>%
  mutate(cum_pct = cumsum(pct_var_exp)) 

Prop_Var_Explained_df %>%
  ggplot(aes(x=PC, y=cum_pct)) +
  geom_point() +
  geom_smooth()

`geom_smooth()` using method = 'loess' and formula = 'y ~ x'

Code

min_cum_pct <- min(Prop_Var_Explained_df$cum_pct)

min_cum_pct

[1] 0.3740717

Code

pc_var2 <- Prop_Var_Explained_df %>%
  filter(cum_pct <= max(0.8, min_cum_pct))

pc_var2 %>%
  head()

# A tibble: 5 × 4
  var_exp pct_var_exp    PC cum_pct
    <dbl>       <dbl> <int>   <dbl>
1   6.73       0.374      1   0.374
2   3.47       0.193      2   0.567
3   1.83       0.102      3   0.669
4   1.24       0.0689     4   0.738
5   0.994      0.0552     5   0.793

Code

ggplot(pc_var2, aes(x = reorder(PC, pct_var_exp), y = pct_var_exp)) +
    geom_bar(stat = "identity") +
    scale_y_continuous(labels = scales::percent) +
    coord_flip() +
    labs(x = "Principal Components", y = "% Variance Explained")

Next let’s get the eigenvectors

Code

rotation_tibble <- as_tibble(A_DATA_2.pca.model$rotation , rownames='Feature')

rotation_tibble %>%
  head()

# A tibble: 6 × 19
  Feature   PC1    PC2    PC3      PC4     PC5     PC6     PC7      PC8     PC9
  <chr>   <dbl>  <dbl>  <dbl>    <dbl>   <dbl>   <dbl>   <dbl>    <dbl>   <dbl>
1 BPXDI3  0.182 -0.251 -0.475  0.0705  -0.0588  0.119  -0.0176  0.0113   0.0643
2 BPXSY3  0.230 -0.345  0.232 -0.00584  0.0517 -0.120  -0.0510  0.117    0.358 
3 BPXDI2  0.189 -0.258 -0.465  0.0716  -0.0632  0.122  -0.0125 -0.00103  0.0182
4 BPXSY2  0.231 -0.349  0.241 -0.00866  0.0462 -0.113  -0.0455  0.0994   0.307 
5 BPXDI1  0.191 -0.253 -0.438  0.0683  -0.0560  0.108  -0.0135 -0.0224  -0.115 
6 BPXSY1  0.229 -0.340  0.253 -0.0216   0.0424 -0.0987 -0.0478  0.0526   0.116 
# ℹ 9 more variables: PC10 <dbl>, PC11 <dbl>, PC12 <dbl>, PC13 <dbl>,
#   PC14 <dbl>, PC15 <dbl>, PC16 <dbl>, PC17 <dbl>, PC18 <dbl>

Get the values per the feature

Code

rotation_tibble_T <- rotation_tibble %>%
  pivot_longer(-Feature, names_to = 'variable', values_to = 'value') 

rotation_tibble_T %>%
  head()

# A tibble: 6 × 3
  Feature variable   value
  <chr>   <chr>      <dbl>
1 BPXDI3  PC1       0.182 
2 BPXDI3  PC2      -0.251 
3 BPXDI3  PC3      -0.475 
4 BPXDI3  PC4       0.0705
5 BPXDI3  PC5      -0.0588
6 BPXDI3  PC6       0.119

Plot the results of the feature’s contribution to the PC - lets do the 1st below:

Code

rotation_tibble_T %>%
  filter(variable == paste0("PC", 1)) %>%
  ggplot(aes(x = Feature, y = value)) +
  geom_bar(stat = "identity") +
  coord_flip() +
  ylab("Relative Importance")

9.6.3.1 proc.pca

We can functionalize the entire above process and enhance the proportion of variance explained graph with a ggplot:

Code

proc.pca <- function(data ){
  
  # fit PCA model 
  data.pca <- prcomp(data, 
                      center=TRUE,
                      scale=TRUE)



 biplot_function <- function(choices = c(1,2) , # these are the things I probably want to pass into biplot
                              arrows_colour = "red",
                              arrows_size = 1,
                              arrows_textsize = 4, # the ... should pass anything else 
                              ...){
    AMR::ggplot_pca(data.pca,
                    choices = choices,
                    arrows = TRUE,
                    arrows_colour = arrows_colour, # I think Red is easier to see on Black
                    arrows_size = arrows_size, # bigger arrows
                    arrows_textsize = 4, #bigger text size 
                    ...)
   }

 
  # Proportion of variance explained
  var_exp <- data.pca$sdev^2
  
  pct_var_exp <- var_exp/sum(var_exp)

  Prop_Var_Explained_df <- as_tibble(cbind(var_exp ,pct_var_exp))

  Prop_Var_Explained_df$PC <- 1:nrow(Prop_Var_Explained_df)

  Prop_Var_Explained_df <- Prop_Var_Explained_df %>%
    mutate(cum_pct = cumsum(pct_var_exp)) %>%
    select(PC, var_exp, pct_var_exp, cum_pct)

  # scree plot 
  scree_plot <- Prop_Var_Explained_df %>%
    ggplot(aes(x=PC, y=cum_pct)) +
    geom_point() +
    geom_smooth()

  # PC_var_Explained_bar
  min_cum_pct <- min(Prop_Var_Explained_df$cum_pct)

  PC_var_Explained_bar <- function(variance_cap = 0.8){
  
    pc_var2 <- Prop_Var_Explained_df %>%
      filter(cum_pct <= max(variance_cap, min_cum_pct))

    PC_var_Explained_bar <- ggplot(pc_var2, aes(x = reorder(PC, pct_var_exp), y = pct_var_exp)) +
      geom_bar(stat = "identity") +
      scale_y_continuous(labels = scales::percent) +
      coord_flip() +
      labs(x = "Principal Components", y = "% Variance Explained")

    return(PC_var_Explained_bar)
    }

  #Feature_Imp_PC
   
   # eigenvectors
  rotation_tibble <- as_tibble(A_DATA_2.pca.model$rotation , rownames='Feature')
    
   # get the values per the feature  
  rotation_tibble_T <- rotation_tibble %>%
    pivot_longer(-Feature, names_to = 'variable', values_to = 'value')

    # here's a nice plot of the feature's contribution to the PC 
  Feature_Imp_PC <- function(PC_Num = 1){
    rotation_tibble_T %>%
      filter(variable == paste0("PC", PC_Num)) %>%
      mutate(Feature = reorder(Feature, value)) %>%
      ggplot(aes(x = Feature, y = value)) +
      geom_bar(stat = "identity") +
      coord_flip() +
      ylab("Relative Importance") +
      labs(title = paste0("PC",PC_Num))
    }

#QED

return(list(PCA_Sum = summary(data.pca) ,
            Prop_Var_Explained_df = Prop_Var_Explained_df,
            scree_plot = scree_plot,
            biplot = biplot_function, 
            PC_var_Explained_bar = PC_var_Explained_bar,
            Feature_Imp_PC = Feature_Imp_PC)
       ) 
}

9.6.3.1.1 test proc.pca

Now we can test our function:

Code

OUTPUT.proc.pca <- proc.pca(PCA.train %>% select(all_of(features_65_num$feature)))

Let’s check out the Relative Feature Importance in PC8, for instance:

Code

OUTPUT.proc.pca$Feature_Imp_PC(8)

Again note how most of the variance is explained by the PC1:

Code

OUTPUT.proc.pca$PC_var_Explained_bar(1)

Also note the high Feature Relative Importance of features like BMXWT , Age and BMXBMI in this graph in Figure below:

Code

OUTPUT.proc.pca$Feature_Imp_PC(1)

and the corresponding magnitude and direction of the vector in the plot in Figure below:

Code

OUTPUT.proc.pca$biplot(c(1,2))  +
  coord_cartesian(ylim=c(-2.5,2.5))

At the same time, note the above magnitude and direction of BPXPLS corresponding to the negative feature relative importance in PC2 in Figure below:

Code

OUTPUT.proc.pca$Feature_Imp_PC(2)

Getting back on track, we recall

Code

OUTPUT.proc.pca$Prop_Var_Explained_df %>%
  filter(3 <= PC & PC <= 7 ) %>%
  kbl() %>%
  kable_paper("striped", full_width = F) %>%
  row_spec(3, bold = T, color = "white", background = "#D7261E")

PC	var_exp	pct_var_exp	cum_pct
3	1.8319212	0.1017734	0.6687171
4	1.2399124	0.0688840	0.7376011
5	0.9940102	0.0552228	0.7928239
6	0.8599465	0.0477748	0.8405987
7	0.8185082	0.0454727	0.8860714

So knowing 5 Principal Components accounts for about 84.3% of the variance of the data observed in the PCA.train dataset.

9.6.4 Modeling with PCs

We will quickly compare models using:

all of the numeric features
the first 5 PCs
5 random features

First, we’ll use the predict to predict the PCAs onto PCA.train, we then attach those predictions to PCA.train with the cbind:

Code

PCA.PCA.train <- cbind(PCA.train, predict(A_DATA_2.pca.model, PCA.train))

PCA.PCA.train %>%
  glimpse()

Rows: 62,105
Columns: 42
$ SEQN                 <dbl> 36818, 9031, 53291, 60723, 34933, 26505, 55789, 1…
$ DIABETES             <dbl> 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0…
$ Gender               <chr> "Female", "Male", "Female", "Female", "Male", "Fe…
$ Race                 <chr> "Other Hispanic", "Black", "White", "Black", "Mex…
$ Family_Income        <chr> NA, NA, "$20,000 to $24,999", "$ 0 to $ 4,999", N…
$ BPXDI3               <dbl> 64.00000, 66.99878, 60.00000, 66.11492, 64.00000,…
$ BPXSY3               <dbl> 104.0000, 121.7824, 106.0000, 118.8599, 106.0000,…
$ BPXDI2               <dbl> 62.00000, 67.00160, 68.00000, 66.05193, 66.00000,…
$ BPXSY2               <dbl> 110.0000, 122.1358, 110.0000, 119.4753, 104.0000,…
$ BPXDI1               <dbl> 70.00000, 67.28744, 64.00000, 65.88837, 56.00000,…
$ BPXSY1               <dbl> 114.0000, 122.5225, 106.0000, 119.5301, 100.0000,…
$ BMXLEG               <dbl> 35.50000, 44.40000, 37.60000, 38.95650, 42.10000,…
$ BPXML1               <dbl> 150.0000, 149.4231, 140.0000, 146.0224, 130.0000,…
$ BPXPLS               <dbl> 62.00000, 71.25887, 66.00000, 76.42917, 110.00000…
$ PEASCTM1             <dbl> 572.0000, 0.0000, 1007.0000, 554.7339, 673.0000, …
$ BMXWAIST             <dbl> 94.40000, 156.00000, 92.00000, 86.11608, 97.00000…
$ BMXBMI               <dbl> 31.92000, 58.13000, 29.55000, 26.99533, 25.76000,…
$ BMXHT                <dbl> 153.7000, 174.6000, 168.4000, 152.4810, 165.3000,…
$ BMXARMC              <dbl> 32.30000, 54.20000, 32.00000, 29.20228, 29.60000,…
$ BMXARML              <dbl> 33.20000, 41.80000, 36.20000, 33.37321, 37.20000,…
$ Poverty_Income_Ratio <dbl> 1.160000, 3.260000, 1.850000, 0.280000, 2.440000,…
$ BMXWT                <dbl> 75.40000, 177.20000, 83.80000, 65.08800, 70.40000…
$ Age                  <dbl> 35, 40, 52, 50, 14, 4, 56, 25, 12, 45, 33, 3, 40,…
$ DIABETES_factor      <fct> 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0…
$ PC1                  <dbl> 0.1618906, 5.4191054, 0.8081946, 0.1253923, -0.72…
$ PC2                  <dbl> 0.88041681, 2.94120994, 1.95130317, -0.05317229, …
$ PC3                  <dbl> 0.13255599, -0.39551539, 0.08674368, 0.26886141, …
$ PC4                  <dbl> 0.56857209, 1.30967314, -0.06766784, 0.65707336, …
$ PC5                  <dbl> 0.32247866, 2.42519764, -0.56585948, 0.79657233, …
$ PC6                  <dbl> 1.42690957, -2.28819159, 1.55727562, 0.62629462, …
$ PC7                  <dbl> 1.11613718, 4.32023643, -0.35276793, -0.34089376,…
$ PC8                  <dbl> 0.0895124633, -0.5565730422, 0.5317360659, -0.567…
$ PC9                  <dbl> -0.64089491, -0.03689855, -0.58800084, -0.2145766…
$ PC10                 <dbl> 0.38161931, 0.13321781, -0.32139189, -0.49231855,…
$ PC11                 <dbl> 0.473591941, -0.078312744, -0.119743858, -0.18399…
$ PC12                 <dbl> 0.1446828607, 0.6681638637, -0.2102899935, -0.000…
$ PC13                 <dbl> 0.1362016900, 0.0179423936, -0.4607317349, 0.0119…
$ PC14                 <dbl> -0.1024173905, 0.0095358839, 0.2226078362, 0.0615…
$ PC15                 <dbl> -0.20946179, -0.42950098, -0.31750191, -0.1606166…
$ PC16                 <dbl> 2.107777e-01, -4.693024e-02, 3.016626e-02, -6.424…
$ PC17                 <dbl> -0.038872720, 0.122516960, -0.001755631, -0.07690…
$ PC18                 <dbl> -0.0683878914, 0.1794237009, 0.0408375138, -0.069…

Recall our features were

Code

features_65_num$feature

 [1] "BPXDI3"               "BPXSY3"               "BPXDI2"              
 [4] "BPXSY2"               "BPXDI1"               "BPXSY1"              
 [7] "BMXLEG"               "BPXML1"               "BPXPLS"              
[10] "PEASCTM1"             "BMXWAIST"             "BMXBMI"              
[13] "BMXHT"                "BMXARMC"              "BMXARML"             
[16] "Poverty_Income_Ratio" "BMXWT"                "Age"

We can make a formula:

Code

features_plus <- paste0(features_65_num$feature, collapse = " + ")
features_plus

[1] "BPXDI3 + BPXSY3 + BPXDI2 + BPXSY2 + BPXDI1 + BPXSY1 + BMXLEG + BPXML1 + BPXPLS + PEASCTM1 + BMXWAIST + BMXBMI + BMXHT + BMXARMC + BMXARML + Poverty_Income_Ratio + BMXWT + Age"

Code

feature_fomula <- paste0("DIABETES_factor ~ ", features_plus)
feature_fomula

[1] "DIABETES_factor ~ BPXDI3 + BPXSY3 + BPXDI2 + BPXSY2 + BPXDI1 + BPXSY1 + BMXLEG + BPXML1 + BPXPLS + PEASCTM1 + BMXWAIST + BMXBMI + BMXHT + BMXARMC + BMXARML + Poverty_Income_Ratio + BMXWT + Age"

Let’s also choose 5 random features for good measure

Code

set.seed(86753094)
feature_rand_5_formula <- paste0("DIABETES_factor ~ ", 
                                 paste0(sample(features_65_num$feature, 5, replace = FALSE ), 
                                        collapse = " + "))
feature_rand_5_formula

[1] "DIABETES_factor ~ BMXLEG + BPXSY3 + Poverty_Income_Ratio + BMXHT + PEASCTM1"

And now we can train our three models:

Code

logit_PCA <- glm(DIABETES_factor ~ PC1 + PC2 + PC3 + PC4 + PC5,
                 data = PCA.PCA.train,
                 family = binomial(link = 'logit'))

logit_features <- glm(as.formula(feature_fomula),
                      data = PCA.PCA.train,
                      family = binomial(link = 'logit'))

logit_rand_5 <- glm(as.formula(feature_rand_5_formula),
                     data = PCA.PCA.train,
                     family = binomial(link = 'logit'))

There is an issue: the test set does not know what it’s PCAs are at this moment, the PCA model was trained on the training set. Therefore, we will need to apply the PCAs model to the test set to get the predicted PCAs:

Code

PCA.PCA.test <- cbind(PCA.test, predict(A_DATA_2.pca.model, PCA.test))

We can utilize our helper from the last chapter,

NOTE THE CHANGES MADE BELOW

we added additional parameters for the target and the level, now this helper-function can be utilized with other data-frames that do not contain the column DIABETES_factor, this will still add on three additional columns to the data frame to be scored probs, pred and pred_factor where pred is set to 1 if over the mean probability score of the target at the level in the training dataset.

Code

logit_model_scorer <- function(my_model, my_data, target , level){ 
  # extracts models name 
  my_model_name <- deparse(substitute(my_model))
  
  enquo_target <- enquo(target)
  
  # store model name into a new column called model
  data.s <- my_data %>%
    mutate(model = my_model_name)
  
  # store the training data someplace
  train_data.s <- my_model$data
  
  # score the training data 
  train_data.s$probs <- predict(my_model, 
                                train_data.s, 
                                'response')
  
  # threshold query
  threshold_value_query <- train_data.s %>% 
                        group_by(!!enquo_target) %>%
                        summarise(mean_prob = mean(probs, na.rm=TRUE)) %>%
                        ungroup() %>%
                        filter(!!enquo_target == level)
  # threshold value                      
  threshold_value <- threshold_value_query$mean_prob
  
  # score test data
  data.s$probs <- predict(my_model, 
                          data.s, 
                          'response')
  
  # use threshold to make prediction  
  data.s <- data.s %>%
    mutate(pred = if_else(probs > threshold_value, 1,0)) %>%
    mutate(pred_factor = as.factor(pred))             
  
  # return scored data 
  return(data.s)
}

And we can get a quick comparison of the ROC Curves

9.6.5 Effectiveness of PCs as features

Code

library('yardstick')


Attaching package: 'yardstick'

The following object is masked from 'package:readr':

    spec

Code

compare_models <- bind_rows(
  logit_model_scorer(logit_PCA, PCA.PCA.test, DIABETES_factor, 1),
  logit_model_scorer(logit_features, PCA.PCA.test, DIABETES_factor, 1),
  logit_model_scorer(logit_rand_5, PCA.PCA.test, DIABETES_factor, 1),
) 


model_AUCS <- compare_models %>%
  group_by(model) %>%
  roc_auc(truth= DIABETES_factor, probs, event_level = "second") %>%
  mutate(model_AUC = paste(model , " AUC : ", round(.estimate,4)))

compare_models %>%
  left_join(model_AUCS) %>%
  group_by(model_AUC) %>%
  roc_curve(truth= DIABETES_factor, probs, event_level = "second") %>%
  autoplot()

Joining with `by = join_by(model)`

In this instance the model with the first 5 PCAs performed better than a model with 5 features chosen at random.

Code

Percent_Diff <- function(x,y){
   return(abs(x-y)/mean(x,y)*100) 
}


percent_diff_auc_Table <- model_AUCS %>%
  select(-model_AUC) %>%
  pivot_wider(names_from = model, values_from = .estimate) %>%
  mutate(percent_diff_auc.all_PCA = Percent_Diff(logit_features, logit_PCA)) %>%
  mutate(percent_diff_auc.PCA_rand_5 = Percent_Diff(logit_PCA, logit_rand_5)) 
  

percent_diff_auc_Table %>%
  glimpse()

Rows: 1
Columns: 7
$ .metric                     <chr> "roc_auc"
$ .estimator                  <chr> "binary"
$ logit_PCA                   <dbl> 0.850824
$ logit_features              <dbl> 0.8815747
$ logit_rand_5                <dbl> 0.782553
$ percent_diff_auc.all_PCA    <dbl> 3.488152
$ percent_diff_auc.PCA_rand_5 <dbl> 8.024109

So there’s only a 3.49% percent difference in Area between the logistic regression model with all of the features and the model with the first 5 PCs, and there is a 8.02% percent difference between the model with the first 5 PCs and a model with 5 features chosen at random.

9.7 k-means Clustering

k-means clustering that aims to partition \(n\) observations into \(k\) clusters in which each observation belonging to the cluster with the nearest mean (cluster centers or cluster centroid), serving as a prototype of the cluster.

Code

set.seed(657)
Sample_Id <- sample(A_DATA_2.Num.impute$SEQN, 
                    nrow(A_DATA_2.Num.impute)*.4, 
                    replace = FALSE)

DATA_65.impute.sample <- A_DATA_2.Num.impute %>%
  filter(SEQN %in% Sample_Id) %>%
  mutate(
    across(
      all_of(features_65_num$feature), 
      \(x){scale(x)}
      )
    )

9.7.1 How do we estimate the number of clusters?

Code

proc.kmeans <- function(data, k = 1:9){

kclusts <-
  tibble(k = k) %>%
  mutate(
    kclust = map(k, ~kmeans(data, .x)),
    glanced = map(kclust, glance),
    augmented = map(kclust, augment, data)
  )

kmeans_model <- function(final_k = 5){
   (kclusts %>%
     filter(k == final_k))$kclust[[1]]
}

id_vars <- colnames(kclusts)

cluster_assignments <- kclusts %>%
  unnest(cols = augmented)

vars <- setdiff(colnames(cluster_assignments), c(id_vars,'.cluster'))

within_cluster_variation_plot <- kclusts %>%
  unnest(cols = c(glanced)) %>%
  ggplot(aes(k, tot.withinss))  +
  geom_line() +
  geom_point() +
  labs(title = "Within Cluster Variation versus number of Clusters")

kmeans.pca <- cluster_assignments %>%
  select(all_of(vars)) %>%
  prcomp()

cluster_assignments_plot <- kmeans.pca %>%
  augment(cluster_assignments) %>%
  ggplot( aes(x = .fittedPC1, y = .fittedPC2, color = .cluster )) +
  geom_point(alpha = 0.8) +
  facet_wrap(~ k) +
  labs(title = "k-means clusterings")

return(list(cluster_assignments_plot= cluster_assignments_plot,
            within_cluster_variation_plot=within_cluster_variation_plot,
            kmeans_model = kmeans_model))
}

Code

library('broom')

tic <- Sys.time()

proc.kmeans.results <- proc.kmeans(DATA_65.impute.sample %>%
                                     select(all_of(features_65_num$feature)), 
                                   k = 3:11)

Warning: There was 1 warning in `mutate()`.
ℹ In argument: `kclust = map(k, ~kmeans(data, .x))`.
Caused by warning:
! Quick-TRANSfer stage steps exceeded maximum (= 1910900)

Code

toc <- Sys.time()

toc - tic

Time difference of 2.338037 secs

Code

proc.kmeans.results$cluster_assignments_plot

Code

cluster_wgss <- function(data, nc=15){ 

clusters <- 1:nc 

wss <- purrr::map_dfr(clusters, 
                      function(N_Clusters){ 
                        wgss = sum(kmeans(data, centers = N_Clusters)$withinss) 
                        
                        tibble(N_Clusters, wgss) 
                        } ) 
}

Code

DATA_65.impute.sample %>%  
  select(all_of(features_65_num$feature)) %>% 
  cluster_wgss(nc=10) %>%        
  ggplot(aes(x= N_Clusters, y= wgss)) + 
  geom_point() + 
  geom_line() +  
  labs(title = "Within group Sum of Squares Plot",
        x="Number of Clusters",
        y="Within groups sum of squares")

Warning: did not converge in 10 iterations

Above, we see a bend in the curve at around 5 so below we will run a kmeans experiment with (\(k\)) centers = 5.

kmeans has an additional options, here I chose 15 for the number of random starting positions:

Code

set.seed(12345)

km <- kmeans(DATA_65.impute.sample %>% select(all_of(features_65_num$feature)) , 
             centers = 5,
             iter.max= 15,
             nstart = 15)

We can now attach the clusters back to the data-frame:

Code

df.cluster <- cbind(DATA_65.impute.sample, cluster=km$cluster)

df.cluster %>%
  select(cluster, all_of(colnames(df.cluster)))  %>%
  head()

  cluster  SEQN DIABETES Gender             Race      Family_Income
1       3 55789        1   Male   Other Hispanic $55,000 to $64,999
2       4 75713        0 Female            Other $ 5,000 to $ 9,999
3       1 15437        1   Male Mexican American               <NA>
4       3 78051        0   Male            Other  $100,000 and Over
5       3  6340        0 Female            Black               <NA>
6       3  4173        0   Male            Black               <NA>
        BPXDI3      BPXSY3       BPXDI2      BPXSY2      BPXDI1       BPXSY1
1 -0.002926798 -0.27887716  0.145535072 -0.43689044  0.45485487  0.146699287
2 -0.315622005 -2.07646920 -0.327163735 -2.19401705 -0.64641716 -2.170554928
3  0.622463615 -1.43447204  0.618233879 -0.56239949  0.76950403 -0.585065202
4 -1.566402832 -0.15047772 -0.799862542 -0.06036331 -0.01711886  0.146699287
5  0.006057295  0.03312412 -0.007940145  0.03221977 -0.02590014 -0.003914424
6  0.622463615  0.36312000  0.460667610  0.06514573  0.45485487  0.268660036
       BMXLEG       BPXML1     BPXPLS    PEASCTM1    BMXWAIST      BMXBMI
1 -0.44639159  0.200775994 -0.5815039 -0.32108201  0.17860359 -0.04536005
2 -1.25743679 -1.346468894  0.6757638  0.89917628 -0.75929332 -0.95733064
3  0.96639683 -0.314972302  0.3165445 -0.23484467  1.27200673  0.82918924
4  0.99255958 -0.314972302 -0.5815039  0.50679641  0.20290144 -0.15346599
5  0.03931988 -0.004366641  0.1754762 -0.07645312 -0.01499759  0.22010027
6  1.82976753  0.200775994  1.0349831  0.81725081 -0.66696150 -0.79101381
       BMXHT     BMXARMC     BMXARML Poverty_Income_Ratio       BMXWT
1  0.6183841  0.37915562  0.49685231            1.1981448  0.28259068
2 -0.6103977 -0.93588713 -0.69156887           -1.3140066 -0.90840454
3  1.0428724  0.86879920  1.19405940            0.1308059  1.26139709
4  1.3869313  0.49107415  0.90883832            1.7708633  0.71381308
5 -0.1554794  0.05770916 -0.06198931           -0.2388719  0.03576730
6  0.9892528 -0.22240649  1.17821378           -1.4051209 -0.05280453
         Age DIABETES_factor
1  0.9736216               1
2 -0.8273815               0
3  0.5233708               1
4  0.3187114               0
5  1.1782810               0
6 -0.5408583               0

9.7.1.1 So what?

We can modify cat_feature_explore from Section ?sec-rewrite-functions-to-gain-speed-ups to create:

Code

proc_chi_square <- function(data, factor, feature){

  enquo_feature <- enquo(feature)
  enquo_factor <- enquo(factor)
  
  tmp <- data %>%
    select(!!enquo_factor, !!enquo_feature) %>%
    collect()
  
   table1 <- table(tmp) 
   
   table2 <- table(tmp %>% select(!!enquo_feature, !!enquo_factor) )
   
   plot_chi_square_residuals <-  vcd::mosaic(table2, gp = vcd::shading_max)
  
   plot_balloon <- gplots::balloonplot(table2, 
                                       main ="Balloon Plot for Gender by Diabetes \n Area is proportional to Freq.")
   
   return( list(Frequency_Table = table2,
                plot_chi_square_residuals = plot_chi_square_residuals,
                plot_balloon = plot_balloon))
   
}

Now let’s run Chi-Square on it:

Code

proc_chi_square(df.cluster, DIABETES, cluster)

$Frequency_Table
       DIABETES
cluster     0     1
      1  6516  1034
      2  3625   875
      3 13768   696
      4  5341    84
      5  6272     7

$plot_chi_square_residuals
        DIABETES     0     1
cluster                     
1                 6516  1034
2                 3625   875
3                13768   696
4                 5341    84
5                 6272     7

$plot_balloon
NULL

9.7.2 Effectiveness of k-means clusters as features

If you’re still skeptical because df.cluster is a sample of A_DATA_2.Num.impute then we can project the clusters onto all of A_DATA_2.Num.impute:

Code

A_DATA_2.Num.impute_scale <- A_DATA_2.Num.impute %>%
  mutate(
    across(
      all_of(features_65_num$feature), 
      \(x){scale(x)}
      ))

Code

library(clue)

cluster <- clue::cl_predict(km,
                             A_DATA_2.Num.impute_scale %>% select(all_of(features_65_num$feature))
                            )

A_DATA_2.Num.impute_scale$.cluster <- factor(as.numeric(as.character(cluster)))

Now run proc_chi_square on it:

Code

proc_chi_square(A_DATA_2.Num.impute_scale, DIABETES, .cluster)

$Frequency_Table
        DIABETES
.cluster     0     1
       1 16182  2674
       2  9128  2115
       3 34395  1805
       4 13330   199
       5 15705    14

$plot_chi_square_residuals
         DIABETES     0     1
.cluster                     
1                 16182  2674
2                  9128  2115
3                 34395  1805
4                 13330   199
5                 15705    14

$plot_balloon
NULL

Above, we can see Diabetics are much more concentrated in Clusters 2, 3, & 4 than the others.

Code

A_DATA_2.Num.impute_scale %>%
  group_by(.cluster) %>%
  summarise(N_Diabetic = sum(DIABETES))

# A tibble: 5 × 2
  .cluster N_Diabetic
  <fct>         <dbl>
1 1              2674
2 2              2115
3 3              1805
4 4               199
5 5                14

9.8 Packages for Automated Exploratory Data Analysis

There are also packages that can assist with automated EDA. Two such packages which we will point to as a reference are DataExplorer and skimr.